I encourage all MX2 students to have a look at the following thread in the MX1 forum:
https://boredofstudies.org/threads/vector-projections-qs-help-plz-ugrent.394192/
The third question sounds simple but I believe it has been set in error as there is no simple solution. The posts in the thread do explore some aspects of the problem and could be adapted to a problem in proof.
Perhaps as something like:
If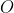 is the origin,
is the origin, 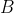 is a variable point satisfying
is a variable point satisfying 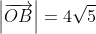 , and
, and 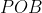 is a triangle of area 10 u2, show that
is a triangle of area 10 u2, show that 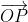 can be located anywhere on the number plane so long as
can be located anywhere on the number plane so long as 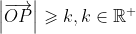 , and find the value of
, and find the value of  .
.
https://boredofstudies.org/threads/vector-projections-qs-help-plz-ugrent.394192/
The third question sounds simple but I believe it has been set in error as there is no simple solution. The posts in the thread do explore some aspects of the problem and could be adapted to a problem in proof.
Perhaps as something like:
If
