Hmm for something like this, maybe try first splitting it into
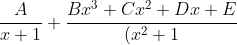^2})
After this, for the second fraction, notice Bx(x^2+1)=Bx^3+Bx, and do the same for the other ones, and rearrange these expressions so that you get some nice fractions that cancel out.
So eventually, in the numerator of the second fraction, you get a (x^2+1) term that cancels out with the denominator, and you get a new fraction..then split that resultant fraction as necessary.