Clueless0182
Member
- Joined
- Feb 9, 2021
- Messages
- 72
- Gender
- Female
- HSC
- 2023
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Thanks for your reply!Would the following working help for Question 10 and Question 11 part (a)?
Question 10:
As the tables are distinguishable, all we need to do is to assign people to each table.
Choose 5 out of 10 to be in the first table:.
Choose 5 out of the remaining 5 to be in the second table:.
After we have chosen who is to be on what table, we must arrange them. There are 4! ways of arranging those on the oak table. There are 4! ways again for the mahogany table.
Question 11:
Part (a):
Assuming the group of 4 rowers as 1 person, group of 3 basketballers as 1 person and the cricketers as 2 separate persons (So, a total of 4 persons)
Number of ways to arrange n people in a round table =
Number of ways to arrange the groups =.
Excluding the number of ways in which the rowers and basketballers will sit together. Assuming basketballers and rowers as one person there are
Hence the number of ways to arrange the groups where rowers and basketballers sit together is 2.
Number of ways to arrange basketballers among their group =
Number of ways to arrange rowers among their group =
Hence, total number of ways is.
I dont really undertand this part. I get how you got 4 but don't understand why. Also if you got 4 why did you then write 2?Excluding the number of ways in which the rowers and basketballers will sit together. Assuming basketballers and rowers as one person there are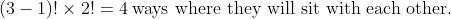
Hence the number of ways to arrange the groups where rowers and basketballers sit together is 2.
No worries!Thanks for your reply!
Q10 makes perfect sense to me.
Regarding Q11,
I dont really undertand this part. I get how you got 4 but don't understand why. Also if you got 4 why did you then write 2?
