I need help with these questions, I'm so confused 
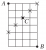
1. The diagram shows a 6 × 4 grid. The aim is to walk from the point A in the top left-hand corner to the point B in the bottom right-hand corner by walking along the black lines either downwards or to the right. A single move is defined as walking along one side of a single small square, thus it takes you ten moves to get from A to B.
Find how many different routes are possible:
I) without restriction,
ii) if you must pass through C
2. Twelve points are arranged in order around a circle.
b) In how many pairs of such triangles are the vertices of the two triangles distinct?
c) In how many such pairs will the triangles: i not overlap, ii overlap?
3. Find how many arrangements of the letters of the word TRANSITION are possible if
a) an N occupies the first but not the last position
b) the letter N is not at either end,
c) the vowels are together.
4. Numbers less than 4000 are formed from the digits 1, 3, 5, 8 and 9, without repetition.
a)How many such numbers are there?
b) How many of them are odd?
c) How many of them are divisible by 5?
d) How many of them are divisible by 3?
1. The diagram shows a 6 × 4 grid. The aim is to walk from the point A in the top left-hand corner to the point B in the bottom right-hand corner by walking along the black lines either downwards or to the right. A single move is defined as walking along one side of a single small square, thus it takes you ten moves to get from A to B.
Find how many different routes are possible:
I) without restriction,
ii) if you must pass through C
2. Twelve points are arranged in order around a circle.
b) In how many pairs of such triangles are the vertices of the two triangles distinct?
c) In how many such pairs will the triangles: i not overlap, ii overlap?
3. Find how many arrangements of the letters of the word TRANSITION are possible if
a) an N occupies the first but not the last position
b) the letter N is not at either end,
c) the vowels are together.
4. Numbers less than 4000 are formed from the digits 1, 3, 5, 8 and 9, without repetition.
a)How many such numbers are there?
b) How many of them are odd?
c) How many of them are divisible by 5?
d) How many of them are divisible by 3?
Last edited: