-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Please help with this chem question (1 Viewer)
- Thread starter mmw
- Start date
Write equation for precipitate formation:
2AgNO3(aq) + K2SO4(aq) --> Ag2SO4(s) +2KNO3(aq)
It is a Q type of calculation:
Ag2SO4(s) < -- > 2Ag+(aq) + SO4 2-(aq)
Q = [Ag+]^2 [SO4 2-]
Our goal to solve the question is to find these 2 concentrations so we can sub it into the Q
A dilution occurs when the two solutions are combined:
For AgNO3 conc
c1v1 = c2v2
(0.10)(100) = c2 (100+100)
c2(AgNO3) = 0.05 mol/L
As each AgNO3 has one Ag+ ion, we can say [Ag+] = 0.05 mol/L
Similarly, if we did this above steps for the K2SO4 solution we will get [SO4 2-] = 0.05 mol/L
Sub into Q:
Q = (0.05)^2 (0.05)
Q = 1.25 x 10^-4
Here Q > Ksp. This means there will be a shift to the left in the equilibrium (Ag2SO4(s) < -- > 2Ag+(aq) + SO4 2-(aq)). If we shift left that means a precipitate is made
2AgNO3(aq) + K2SO4(aq) --> Ag2SO4(s) +2KNO3(aq)
It is a Q type of calculation:
Ag2SO4(s) < -- > 2Ag+(aq) + SO4 2-(aq)
Q = [Ag+]^2 [SO4 2-]
Our goal to solve the question is to find these 2 concentrations so we can sub it into the Q
A dilution occurs when the two solutions are combined:
For AgNO3 conc
c1v1 = c2v2
(0.10)(100) = c2 (100+100)
c2(AgNO3) = 0.05 mol/L
As each AgNO3 has one Ag+ ion, we can say [Ag+] = 0.05 mol/L
Similarly, if we did this above steps for the K2SO4 solution we will get [SO4 2-] = 0.05 mol/L
Sub into Q:
Q = (0.05)^2 (0.05)
Q = 1.25 x 10^-4
Here Q > Ksp. This means there will be a shift to the left in the equilibrium (Ag2SO4(s) < -- > 2Ag+(aq) + SO4 2-(aq)). If we shift left that means a precipitate is made
specificagent1
Well-Known Member
- Joined
- Aug 24, 2021
- Messages
- 1,969
- Gender
- Male
- HSC
- 2021
What is Q actually measuring?Write equation for precipitate formation:
2AgNO3(aq) + K2SO4(aq) --> Ag2SO4(s) +2KNO3(aq)
It is a Q type of calculation:
Ag2SO4(s) < -- > 2Ag+(aq) + SO4 2-(aq)
Q = [Ag+]^2 [SO4 2-]
Our goal to solve the question is to find these 2 concentrations so we can sub it into the Q
A dilution occurs when the two solutions are combined:
For AgNO3 conc
c1v1 = c2v2
(0.10)(100) = c2 (100+100)
c2(AgNO3) = 0.05 mol/L
As each AgNO3 has one Ag+ ion, we can say [Ag+] = 0.05 mol/L
Similarly, if we did this above steps for the K2SO4 solution we will get [SO4 2-] = 0.05 mol/L
Sub into Q:
Q = (0.05)^2 (0.05)
Q = 1.25 x 10^-4
Here Q > Ksp. This means there will be a shift to the left in the equilibrium (Ag2SO4(s) < -- > 2Ag+(aq) + SO4 2-(aq)). If we shift left that means a precipitate is made
What is the method in calculating Q?
Also Why is it that if
Q > ksp = Precipitate
Q < ksp = no precipitate
Q = ksp = no precipitate but saturated?
Thank you so much!Write equation for precipitate formation:
2AgNO3(aq) + K2SO4(aq) --> Ag2SO4(s) +2KNO3(aq)
It is a Q type of calculation:
Ag2SO4(s) < -- > 2Ag+(aq) + SO4 2-(aq)
Q = [Ag+]^2 [SO4 2-]
Our goal to solve the question is to find these 2 concentrations so we can sub it into the Q
A dilution occurs when the two solutions are combined:
For AgNO3 conc
c1v1 = c2v2
(0.10)(100) = c2 (100+100)
c2(AgNO3) = 0.05 mol/L
As each AgNO3 has one Ag+ ion, we can say [Ag+] = 0.05 mol/L
Similarly, if we did this above steps for the K2SO4 solution we will get [SO4 2-] = 0.05 mol/L
Sub into Q:
Q = (0.05)^2 (0.05)
Q = 1.25 x 10^-4
Here Q > Ksp. This means there will be a shift to the left in the equilibrium (Ag2SO4(s) < -- > 2Ag+(aq) + SO4 2-(aq)). If we shift left that means a precipitate is made
icycledough
Well-Known Member
- Joined
- Aug 5, 2021
- Messages
- 784
- Gender
- Male
- HSC
- 2020
I believe it's to do with the amount of dissolution. So Q essentially measures the same variable as Ksp, which is the concentration of products (gaseous or aqueous states) divided by the concentration of reactants, but it is at a specific point in time. So if Q is less than Ksp, this means the solution is unsaturated and more solid will continue to dissolve until the system reaches equilibrium, which occurs when Q = Ksp. Alternatively, if Q is greater than Ksp, then the solution is 'supersaturated', and so solid will precipitate until Q = Ksp (so reverse process). When Q = Ksp, the rate of dissolution is equal to the rate of precipitation, so there will be no net change in the amount of dissolved solid. Thus, there won't be a 'visible' precipitateWhat is Q actually measuring?
What is the method in calculating Q?
Also Why is it that if
Q > ksp = Precipitate
Q < ksp = no precipitate
Q = ksp = no precipitate but saturated?
Q is called the reaction quotient. It is used to describe the ratio of products to reactants in a reversible reaction. K (the equilibirum constant) is a specific type of Q, when a system is at equilibrium.What is Q actually measuring?
What is the method in calculating Q?
Also Why is it that if
Q > ksp = Precipitate
Q < ksp = no precipitate
Q = ksp = no precipitate but saturated?
For HSC this should be enough of an explanation for those 3 statements:
The system is trying to reach equilibrium, so it wants to make Q = K, because when the reaction quotient is equal to the equilibrium constant we say the system is at equilibrium.
The equilibrium constant is a set value for a certain temperature and so the only way to make Q = K, is to change Q.
Using an equation and actual variables makes this easier to understand. Take the equation:
R < -- > P
Q = [P] / [R]
If Q > K, then for the system to reach equilibrium the value of Q must decrease to meet the value of K. The only way to decrease Q is to decrease [P] term and increase [R] term.
For this to occur the equilibrium must shift to the left to increase [R] and decrease [P]
In this case of a solubility equilibrium, shifting to the left means you are shifting towards and making the precipitate.
If Q < K, the Q must increase to meet the value of K. To increase Q, increase [P] term and decrease [R] term. This is the equilibrium shifting to the right i.e. the dissolution process is still favoured and so the solution has not reached saturation
If Q = K, the system is at equilibrium. It won't have any reason to shift either way unless you disturb the equilibrium and change something
One small addendum about these specific (precipitation / solubility) systems...
If I mix (in this case) silver nitrate and potassium sulfate and a precipitate forms, I have a solubility equilibrium where
and the concentrations are related by Ksp = [Ag+]2[SO42-] is constant at constant temperature.
However, if a precipitate does not form (and thus, Q < Ksp), there is not an equilibrium system here. This is because an equilbrium system must contain a reversible chemical reaction, and the rate of precipitation is zero (as no precipitate is forming) and the rate of dissolution is zero (as there is no solid to dissolve).
An equilibrium system reaches the point of being at equilibrium when the rates of the forward and reverse reactions are equal and non-zero.
If this was not the case then any irreversible reaction could be considered an equilibrium where the reverse reaction has a rate of zero, and thus to reach being "at equilibrium" when it reaches completion. However, applying Le Chatelier's Principle to predict changes in such a situation would make no sense. I can't burn petrol to drive my car, reach completion by running out of fuel, the pump exhaust gases back into the engine mixed with water and use Le Chatelier's Principle to predict that some of the petrol will be re-formed suddenly.
If I mix (in this case) silver nitrate and potassium sulfate and a precipitate forms, I have a solubility equilibrium where
Ag2SO4(s) <----> 2Ag+(aq) + SO42-(aq)
and the concentrations are related by Ksp = [Ag+]2[SO42-] is constant at constant temperature.
However, if a precipitate does not form (and thus, Q < Ksp), there is not an equilibrium system here. This is because an equilbrium system must contain a reversible chemical reaction, and the rate of precipitation is zero (as no precipitate is forming) and the rate of dissolution is zero (as there is no solid to dissolve).
An equilibrium system reaches the point of being at equilibrium when the rates of the forward and reverse reactions are equal and non-zero.
If this was not the case then any irreversible reaction could be considered an equilibrium where the reverse reaction has a rate of zero, and thus to reach being "at equilibrium" when it reaches completion. However, applying Le Chatelier's Principle to predict changes in such a situation would make no sense. I can't burn petrol to drive my car, reach completion by running out of fuel, the pump exhaust gases back into the engine mixed with water and use Le Chatelier's Principle to predict that some of the petrol will be re-formed suddenly.
Also, another way of thinking about Q:
For a system, aA + bB <---> cC + dD, the condition for being at equilibrium is that Rate Fwd = Rate Rev > 0.
For mathematical reasons that we don't deal with, this condition is equivalent to
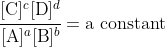
but this applies only at equilibrium.
We define the equilibrium constant, K, as the constant value found from this expression. The fraction of concentrations, however, is variable, it changes as the system moves, and so we define it as the reaction quotient, Q. The condition for a system to be at equilibrium is consequently that Q = K, as at that time the concentrations have the values where the system is at equilibrium. Though we teach it backwards, the consequence here is that it follows that
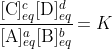
at equilibrium only. If the system is not at equilibrium then
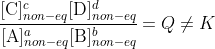
Put another way, Q is a function of several variables (the concentrations in its expression) and K is a constant value of that function that happens to have a useful significance, just as I can make an equation for the area of a field based on given information and then seek the value that corresponds to its maximum.
Le Chatelier's Principle disturbances can then be examined as situations where a change has caused (usually) the value of Q to move away from K, and the system will shift so as to return to having Q = K. This also means that the concentrations at equilibrium that we substitute to find K are not unique, and there are other combinations of concentrations that will result in Q equalling K.
For a system, aA + bB <---> cC + dD, the condition for being at equilibrium is that Rate Fwd = Rate Rev > 0.
For mathematical reasons that we don't deal with, this condition is equivalent to
but this applies only at equilibrium.
We define the equilibrium constant, K, as the constant value found from this expression. The fraction of concentrations, however, is variable, it changes as the system moves, and so we define it as the reaction quotient, Q. The condition for a system to be at equilibrium is consequently that Q = K, as at that time the concentrations have the values where the system is at equilibrium. Though we teach it backwards, the consequence here is that it follows that
at equilibrium only. If the system is not at equilibrium then
Le Chatelier's Principle disturbances can then be examined as situations where a change has caused (usually) the value of Q to move away from K, and the system will shift so as to return to having Q = K. This also means that the concentrations at equilibrium that we substitute to find K are not unique, and there are other combinations of concentrations that will result in Q equalling K.

