Oh, I forgot about the rational part. Since its rational, we need to have the conjugate even for the real solution (in order to thus make a rational factor, resulting in a rational polynomial).
Was reading it as 'real' for some reason.
This is dubious and quite hard to prove.
If anyone is interested, you need to basically know about minimal polynomials and algebraic numbers (its pretty cool).
Basically, each complex (and real!) number is either "algebraic" or "transcendental". What that means is this: an
algebraic number is a number x for which there exists a
polynomial with rational coefficients with x as a zero. So thus, 1 is algebraic, since 1 is a root of x-1. -1/2 is also algebraic, since it is a root of 2x+1. Similarly, the cube root of 2 is algebraic: it is a zero of

, and the number

is algebraic, since its a root of

. Also, 1+i is algebraic, as its a root of

. By contrast, it is INCREDIBLY difficult to prove, but pi and e are not algebraic, so we call them
transcendental. That's basically saying, neither pi nor e are the root of any polynomial (so cant be expressed as anythign like a surd). Essentially algebraic numbers are "generalised surds".
Anyway Im going to define, for each algebraic number, its
minimal polynomial as the
non-zero, monic polynomial with rational coefficients of the smallest degree with that algebraic number as a zero.
It isnt very hard to prove that for each algebraic

, the minimal polynomial is unique: suppose there were two minimal polynomials for some fixed

, call them P and Q. Now consider
 = P(x) - Q(x))
. Clearly as
 = 0, Q(\alpha) = 0)
then
 = 0)
hence

is a root of R. Clearly as P and Q are rational polynomials so is R. Further, P and Q are distinct, so R is nonzero, and also P and Q must be monic and have the same degree (for them both to classify as the "minimal polynomial", otherwise one would clearly classify and the other wouldnt). SInce they're both monic and the same degree, when you subtract them the leading term cancels out, so R has a smaller degree than P or Q. Combine all this information together, and R meets the classifications for

's minimal polynomial EXCEPT it has an even smaller degree. Contradiction, right? So the minimal polynomial is UNIQUE.
Now even cooler, Im gonna claim this. I claim that, if
)
is the minimal polynomial of

and
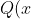)
is some rational non-zero polynomial with

as a root, then
)
is a factor of
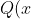)
. This is basically a MUCH strengthened form of the factor theorem for rational coefficient polynomials. Its really easy to prove as well. Use the division/remainder/Euclidean algorithm to write:
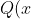 = D(x)P(x) + R(x))
for some rational polynomials D and R, where the degree of R is either zero or strictly less than the degree of P. Then since
 = 0)
and
=0)
, subbing that in you get
 = 0)
. Now R has degree less than P, so if R were nonzero, then R would be a rational polynomial having

as a root with a degree less than the minimal polynomial. Contradiction, right? So R has to be the zero polynomial. It follows that
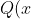 = D(x)P(x))
and thus that P is a factor of Q. MUUUUCH stronger version of the factor theorem.
Now in this question. Suppose

is the root of some rational polynomial say Q. The minimal polynomial of that can't be degree 0 or 1 obviously, so it has to be degree 2, and lo and behold

has that number as a zero and its degree 2, so

is the minimal polynomial of

. Applying what we proved above,

must then divide our mystery polynomial Q. But

also has as a root

. So we've proved

is a root implies

is a root.
If you think about it then, this sorta then implies that algebraic numbers come in sorta "generalised conjugate sets", corresponding to groups of numbers that share the same minimal polynomial. Minimal polynomials then start to work a hell of a lot like prime numbers actually, which is really neat (indeed every minimal polynomial is an irreducible). Also nothing here we proved restricts this to working for just rational polynomials. In any ring where you can define a euclidean algorithm (dunno if my vocabulary is perfectly accurate here), you have stuff like this working. Its all pretty neat

This is all a bit sorta complicated, but tbh I dont know any other reason to justify any sort of "conjugate root theorem" operating on rational numbers. You totally don't learn it at school, partially coz nobody would ever be bothered to prove it for you. Im not entirely sure if you can quote it either. Most maths teachers though are probably honestly not knowledgeable enough to pick up on the subtlety though.

