23. By considering their prime factorisations, find the number of positive divisors of:
(a) 23 × 32 (b) 1 000 000 (c) 315 000 (d) 2a × 5b × 13c
24. (a) The six faces of a number of identical cubes are painted in six distinct colours. How
many different cubes can be formed?
(b) A die fits perfectly into a cubical box. How many ways are there of putting the die
into the box?
23. (a) Prime factorisation of
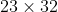
is
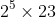
.
Hence to make each positive divisor of
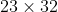
, we can choose to take either 0 lots of 23, or 1 lot of 23 (so
2 possibilites for 23) AND either 0 lots of 2, 1 lot of 2, 2 lots of 2,..., or 5 lots of 2 (so
6 possibilities for 2). (Note that when we take 0 lots of both prime factors 23 and 2, the divisor made is
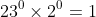
. In general, taking
n lots of 23 and
m lots of 2 gives us the divisor
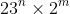
.)
Therefore, the answer to this question is
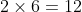
.
(b) and (c) – do the same type of thing. Write the prime factorisation of the number in question, and look at the powers of the prime factors, and then deduce how many possibilities there are for each prime factor, then multiply them.
For (d), we're not told anything about
a,
b or
c, so we can't give a definitive number as our answer.
24. (a) We can just let the top face be Colour A (since Colour A has to go somewhere, so just make the face it goes on be the "top" one).
Then there are
5 choices of colour for the face opposite Colour A (the "bottom" face).
Now, we have 4 colours remaining, and we can put one of these on any of the remaining faces due to symmetry. After putting this colour (call it Colour C) on one of the other faces, we have
3 choices of colour remaining for the face opposite Colour C. After putting a colour D opposite Colour C, we have two remaining faces and
2 remaining colours. Note that this means there are two ways left to colour the cube, and each of these ways makes the cube different (you may have to visualise it to see that the two different ways to colour the cube really will be different).
Answer is
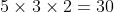
ways.
(b) This surely depends on whether the faces of the cubical box are distinguishable. Presumably the top and bottom faces are, since one has a lid probably, and the other is opposite the lid, but are the remaining faces identical? If they ARE identical, the answer should just be 6 (since there's 6 ways to choose which face of the die to put on the bottom).
If the box's faces are NOT identical, then the answer should be
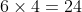
I think. (
6 ways to choose the face of the die to put on the bottom, and then after that
4 ways to choose which face of the die is lined up with Face A of the box, where Face A is one of the faces that is neither the top nor bottom).
