Hellooooooooo  I thought this may be useful for tomorrow or at least it would not hurt to know it, and it's actually quite simple
I thought this may be useful for tomorrow or at least it would not hurt to know it, and it's actually quite simple  well the question and proof is as follows;
well the question and proof is as follows;
Question is prove by mathematical induction for
for 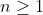
Proof:
It is obviously true for n=1, therefore test for n=2
 , this is the diagonal of the parallelogram formed by the sides
, this is the diagonal of the parallelogram formed by the sides  and
and  . Therefore, by definition of a triangle, the third side of a triangle is always less then the sum of the other two, unless the triangle is flat, meaning the vertices are collinear, this is when
. Therefore, by definition of a triangle, the third side of a triangle is always less then the sum of the other two, unless the triangle is flat, meaning the vertices are collinear, this is when  occurs.
occurs.
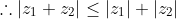
Therefore statement is true for n=1 and n=2
Assume statement is true for n=k
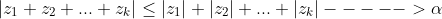
and let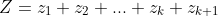
Prove the statement is true for n=k+1
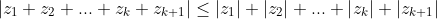
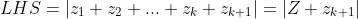
 as seen for when proving for n=2
as seen for when proving for n=2
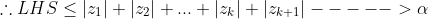
Therefore statement is true for n=k+1, if it is true for n=k. Therefore statement is true for
NB: the equality occurs when for when are colliner, in other words, when
are colliner, in other words, when =arg(z_{2})=...=arg(z_{n})) .
.
Question is prove by mathematical induction
Proof:
It is obviously true for n=1, therefore test for n=2
Therefore statement is true for n=1 and n=2
Assume statement is true for n=k
and let
Prove the statement is true for n=k+1
Therefore statement is true for n=k+1, if it is true for n=k. Therefore statement is true for
NB: the equality occurs when for when
