Have you learnt about the arithmetic/geometric mean inequality yet? It usually looks something like
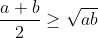
. This can be extended to
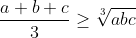
,
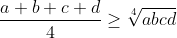
etc.
There's a shortcut to the question using this method:
^3 \geq \left (\sqrt[3]{abc}\right )^3 \rightarrow \frac{(a+b+c)^3}{27} \geq {abc} \rightarrow (a+b+c)^3 \geq {27abc} )
However, since the question asks you to expand, you can collect the 'like' terms of
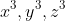
,
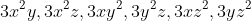
and
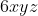
, and do a similar process. You should end up with
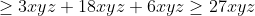
.
Hopefully you find this helpful