How do I do Q10? Thanks
Attachments
-
743.1 KB Views: 54
Are you having trouble with 10 i) or 10 ii)How do I do Q10? Thanks
I *think* you would start by basically putting in the quadratic formula:I'm stuck for part ii). For part i) I put "If the equation a^2x+bx+cx has at least one integer solution, then either a,b or c is even"
I'm not too sure if it's right or not.
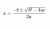
Part i) is correct however I would avoid the use of either or. This because wither or can be taken mean exclusive or.I'm stuck for part ii). For part i) I put "If the equation a^2x+bx+cx has at least one integer solution, then either a,b or c is even"
I'm not too sure if it's right or not.
