Would the following working help with Question 15?
Let the digits of a 4-digit number n be a, b, c, d.
That is,
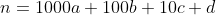
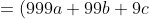+(a+b+c+d))
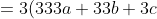+(a+b+c+d)) Part 1:
Part 1:
If n is divisible by 3, then
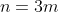
for some integer m.
Therefore:
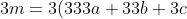+(a+b+c+d))
=3(m-333a-33b-3c))
Therefore the sum of the digits (𝑎 + 𝑏 + 𝑐 + 𝑑) is a multiple of 3.
Part 2:
If the sum of the digits is a multiple of 3, then (𝑎 + 𝑏 + 𝑐 + 𝑑) = 3𝑘 for some integer 𝑘.
Therefore:
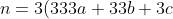+3k)
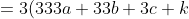)
Therefore 𝑛 is divisible by 3. We have now proved the result in both directions, so a 4-digit number is divisible by 3 if and only if the sum of its digits is divisible by 3.