Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Hello all,
I decided to investigate a function that I thought of:
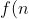 = \begin{cases}$Sum of digits$ \ \ $if$ \ n \ $is prime$ \\ $Sum of prime factors$ \ \ $if$ \ n \ $is composite$ \end{cases} )
i.e. n=14
14 -> 9 -> 6 -> 5
Then I decided to iterate f(n), and as expected, if you keep doing it long enough, you will end up with 1,2,3,5 or 7.
It turns out 1 and 3 can only appear once with a beginning n.
So if you iterate f(n) for all numbers from 0 to 1000, you get ~290 5's that appear.
I decided to investigate the amount of times that '5' appears, it would appear to me that the ratio between the number of numbers checked, and number of times 5 appears, will be periodic.
Indeed, this turns out to be the case:
Basically, I was trying to find (k/n) where k is the number of times 5 appears when you iterate all numbers from 1 to n.
n is the number we try, so if we say n=10
Then: try k=1, iterate, we get 1
try k=2, iterate, we get 2
try k=3, iterate, we get 3
try k=4, iterate, we 4
try k=5, iterate, we get 5
try k=6; iterate, we get 5
try k=7, iterate, we get 7
try k=8, iterate, we get 5
try k= 9, iterate, we get 5
try k=10, iterate, we get 7
So 5 appears 4 times, out of 10 times, so I would record 4/10
Using this code (java):
http://pastebin.com/V9kdKuBs
I got the following data: (~9300 lines of a .txt file)
https://www.dropbox.com/s/0e3yjkau7ff31d1/nums.txt
I put this into excel, and I tried to get good graph, to graph these results, I got:

Unfortunately, I think Eclipse had stopped after line 9300 (even though I told the program to do it for 10000 times), so I cannot get a larger sample space
But it looks to me, to be a steady increase (after the initial expected weirdness)
Now, that graph is ONLY if it ends in 5
I also wanted to get a feeling of what other results we can get.
So if we iterate all numbers from 1 to 101
1 appears 1 time
2 appears 28 times
3 appears 1 times
5 appears 24 times
7 appears 24 times
And if we iterate from 1 to 1001 we get similar ratios.
I have many questions
1) Is it possible to prove mathematically, whether the ratio of the number of times 5 appears, is periodic but is eventually increasing? Perhaps to some limiting value of 1/3?
2) What properties can be derived from such an iterating function
I decided to investigate a function that I thought of:
i.e. n=14
14 -> 9 -> 6 -> 5
Then I decided to iterate f(n), and as expected, if you keep doing it long enough, you will end up with 1,2,3,5 or 7.
It turns out 1 and 3 can only appear once with a beginning n.
So if you iterate f(n) for all numbers from 0 to 1000, you get ~290 5's that appear.
I decided to investigate the amount of times that '5' appears, it would appear to me that the ratio between the number of numbers checked, and number of times 5 appears, will be periodic.
Indeed, this turns out to be the case:
Basically, I was trying to find (k/n) where k is the number of times 5 appears when you iterate all numbers from 1 to n.
n is the number we try, so if we say n=10
Then: try k=1, iterate, we get 1
try k=2, iterate, we get 2
try k=3, iterate, we get 3
try k=4, iterate, we 4
try k=5, iterate, we get 5
try k=6; iterate, we get 5
try k=7, iterate, we get 7
try k=8, iterate, we get 5
try k= 9, iterate, we get 5
try k=10, iterate, we get 7
So 5 appears 4 times, out of 10 times, so I would record 4/10
Using this code (java):
http://pastebin.com/V9kdKuBs
I got the following data: (~9300 lines of a .txt file)
https://www.dropbox.com/s/0e3yjkau7ff31d1/nums.txt
I put this into excel, and I tried to get good graph, to graph these results, I got:

Unfortunately, I think Eclipse had stopped after line 9300 (even though I told the program to do it for 10000 times), so I cannot get a larger sample space
But it looks to me, to be a steady increase (after the initial expected weirdness)
Now, that graph is ONLY if it ends in 5
I also wanted to get a feeling of what other results we can get.
So if we iterate all numbers from 1 to 101
1 appears 1 time
2 appears 28 times
3 appears 1 times
5 appears 24 times
7 appears 24 times
And if we iterate from 1 to 1001 we get similar ratios.
I have many questions
1) Is it possible to prove mathematically, whether the ratio of the number of times 5 appears, is periodic but is eventually increasing? Perhaps to some limiting value of 1/3?
2) What properties can be derived from such an iterating function
