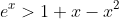View attachment 35309
Hey, can somene help me with this question and in the working out please explain why each step was done because my calculus skills are a little bad, thanks in advanced
i)
This is the same as showing
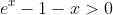
for x > 0. Let h(x) = e^x - 1 -x
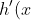 = e^x - 1)
for x > 0
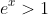
hence for x>0;

therefore
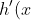 )
is positive for x > 0 and this implies
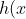 )
is solely increasing for x > 0
 = e^0 - 1 - 0 = 1 - 1 - 0 = 0)
Therefore h(x) > 0 for x > 0 ( as h(x) is increasing for domain (x,infinity) and has a range of (0, infinity) )
ii)
to show a function is concave up for all x,
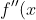 > 0 )
 = e^x - 1 - x + x^2 )
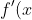 = e^x - 1 + 2x )
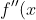 = e^x + 2 )

Hence f(x) is concave up for all x as f''(x) > 0 for all x
iii)
This is similar to the reasoning in 1), as it is proven that the second derivative is increasing for all x so now we just have to check f'(x) at x = 0
 = e^0 - 1 + 2(0) = 1 - 1 = 0 )
Hence
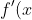 > 0)
for x > 0 as f''(x) is increasing for all values of x and f'(x) has range (0,infty) given x > 0
Now this is just the same process for f(x).
 = e^0 - 1 - 0 + 0 = 0)
Therefore f(x) > 0 for x > 0 as f'(x) is increasing for x > 0 and f(x) has range (0,infty) given x > 0
f(x) > 0 so;