Ok... didn't think about that one. Thanks.
To really confirm for some classes of functions, say Polynomials, you could actually differentiate the function until it reduces to a constant and by observing whether that constant is positive, negative, or equal to 0, we can immediately observe its 'nature'.
We have 3 cases essentially, quite similarly to how we have 3 cases for the discriminant being less than 0, equal to 0, or greater than 0.
Case #1
Suppose we have some function f satisfying the following:
 = 0 $ where $ n \in \left [ 2,2k-1 \right ] $ and $ k,m,n \in \mathbb{N})
and
 < 0 )
then the point
\right ))
is a minimum but not necessarily
) \forall x \in \mathbb{R}) Case #2
Case #2
Suppose we have some function f satisfying the following:
 = 0 $ where $ n \in \left [ 2,2k \right ] $ and $ k,m,n \in \mathbb{N})
and
 \in \mathbb{R} $ and is non-zero.$ )
then the point
\right ))
is an inflexion point.
Case #3
Suppose we have some function f satisfying the following:
 = 0 $ where $ n \in \left [ 2,2k-1 \right ] $ and $ k,m,n \in \mathbb{N})
and
 > 0 )
then the point
\right ))
is a minimum but not necessarily
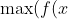) \forall x \in \mathbb{R})