Smile12345
Active Member
- Joined
- May 30, 2013
- Messages
- 827
- Gender
- Undisclosed
- HSC
- 2014
Hello All. 
Could someone please show me the steps for the following question?
'Use one application of the trapezoidal rule to approximate:
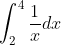
Thanks in advance.
Could someone please show me the steps for the following question?
'Use one application of the trapezoidal rule to approximate:
Thanks in advance.
