R = 8.314 J K
-1 mol
-1 is the value in SI units. It works for:
- P in Pa, V in m3, n in mol, T, in K
- P in kPa, V in L = dm3, n in mol, T in K
This is the standard value which relates to
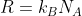
R = 0.08206 L atm K
-1 mol
-1 works for:
- P in atm, V in L, n in mol, T in K
If given a volume in some other unit (like mL or cm
3), convert to L or m
3 as appropriate. If given a pressure in some other unit (ie. 747 mmHg), convert to a suitable pressure unit and apply above...
If given a temperature not in K, convert to K. The ideal gas law and underlying theory
requires a thermodynamic temperature with a zero that is physically meaningful and corresponding to absolute zero. You cannot have a temperature in Celsius and use PV = nRT because Charles' Law tells us that V is proportional to T only if T = 0 corresponds to the theoretical V = 0 limit for a gas... in other words, if T is in Celsius then
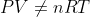
.
The ideal gas law can be modified to uses masses in kg rather than chemical amount in moles, but this also means the equation becomes
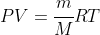
with the above R values, or a change to PV = mRT with R a gas constant with units of g or kg. (Note: SI would say mas must be in kg, but since we seek moles and M is usually in g mol
-1, using m in g is usually appropriate. As with all cases, keeping track of units means making sure that they suit the situation rather than applying blanket rules blindly.)
You can have an R in bar or other units, but it is generally easier to change to P to atm or kPa or Pa and use the above Rs.
Addendum / Note: A link above gives R = 8.314 L kPa K
-1 mol
-1. This is the same as R = 8.314 J K
-1 mol
-1 as, first:
- 1 J = 1 N m
- 1 m3 Pa = 1 3 N m-2 = 1 N m
- So, 1 J = 1 m3 Pa
Now, looking at the units of R:
- 1 L = 1 dm3 = (0.1 m)3 = 10-3 m3
- 1 kPa = 103 Pa
- So, 1 L kPa = 10-3 . 103 m3 Pa = 1 m3 Pa = 1 J
- And thus, 1 L kPa K-1 mol-1 = 1 J K-1 mol-1
This is why I don't bother to list R with two sets of units (and nor do most data sheets) and just recognise that R will work with either the combination (P in kPa, V in L / dm
3) or the SI option (P in Pa, V in m
3).

