A circular cylinder of height 6 cm and base radius 4cm sits on a table with its axis vertical. A point source of light moves vertically upwards at a speed of 3cm/s above the central axis of the cylinder, thus casting a circular shadow on that table. Find the rate at which the radius of the shadow is decreasing when the light is at distance 4 cm above the top of the cylinder.
Define a height axis,
y, along the central axis of the cylinder, taking
y = 0 at the top and placing the light source at
y =
h above the cylinder. When
h > 0, the light casts a shadow of radius i cm from the axis. We are told that
h is increasing at
dh/
dt = 3 cm/s, and
r decreases as this happens,, and we seek
dr/
dt when
h = 4 cm.
Drawing a cross-section of the cylinder and surrounds, with the light moving vertically along the
y axis. At a height of
h cm, the beam of light that touches the rim of the cylinder at the top casts a shadow of
r cm radius, and thus extends (
r - 4) cm beyond the cylinder. There are a pair of similar triangles (AA) in which
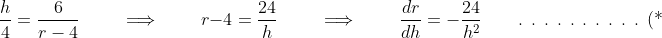})
 and as $\frac{dh}{dt} = +3$ cm/s is given} \\ \\ \text{Thus, when $h = 4$ cm:} \qquad \frac{dr}{dt} &= -\frac{24}{4^2} \times 3 = - \frac{6 \times 3}{4} \\ &= -\frac{9}{2}\ \text{cm/s} \end{align*})
So, the radius of the shadow is decreasing at 4.5 cm/s when the light is 4 cm above the top of the cylinder.
