@kpad5991,
the answer that you have given is incorrect for part (a). If the bottle was originally 4:1 in undiluted cordial to water, then the amount of the undiluted cordial was initially four-fifths of 250 mL (and thus 200 mL) and so, after 100 mL of
mixture is drunk, there must be more than 100 mL of undiluted cordial remaining. So, (a) can't be 96 mL. However, the answer given to be is the answer that follows from (a) had (a) been correct, so the second part of the answer is an error carried forward and thus should gain credit for part (b) in an exam situation.
--- Full answer ---
The 250 mL of mixed cordial in the bottle has a ratio of unmixed cordial to water of 4:1. He drinks 100 mL of the mixed cordial, so after that there is 150 mL of mixed cordial left, still in the 4:1 ratio. So, in that 150 mL, there are
} \quad = \quad \frac{4}{4+1} \times 150 \quad = \quad \frac{4}{5} \times 150 \quad = \quad 120\ \text{mL})
and
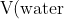} \quad = \quad \frac{1}{4+1} \times 150 \quad = \quad \frac{1}{5} \times 150 \quad = \quad 30\ \text{mL})
You could check this is accurate by applying the 4:1 ratio to the original 250 mL of mixed cordial to find that it was 200 mL of undiluted cordial and 50 mL of water. The same ratio applied to the 100 mL that was drunk shows that this consumed amount consisted of 80 mL of undiluted cordial and 20 mL of water. Hence, the amount remaining is 150 mL made up of 200 - 80 = 120 mL of undiluted cordial and 50 - 20 = 30 mL of water.
He now adds 100 mL of water to the bottle, refilling it to a 250 mL total volume, with the volume of undiluted cordial still 120 mL but the water having increased from 30 mL to 30 + 100 = 130 mL.
So, the amount of undiluted cordial in the drink bottle after the water is added is 120 mL (the answer to the first part) while the fraction of the drink bottle that is cordial has decreased from four-fifths to
}}{\text{V(mixed cordial)}} \\ &= \quad \frac{120}{250} \\ &= \quad \frac{12}{25} \end{align*})
Though it was not requested, the ratio of undiluted cordial to water (which was 4:1 initially) has decreased to
}}{\text{V(water)}} \\ &= \quad \frac{120}{130} \\ &= \quad 12:13 \end{align*})
