Let's do this properly.
^{n}}dx=\int_{0}^{1}x^{2}\left(1+x^{2}\right)^{-n}dx)
After a painstaking battle, I have found that this question can easily get overcomplicated by the student.
The first step integrate
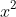
By doing so we will have
^{-n}\right]_{0}^{1})
Sub in x=1 and we will have
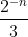
and x=0 will give us 0.
Fear not have faith in yourself.
Now we will be differentiating
^{-n})
The chain rule is your friend
^{-n}=-2nx\left(1+x^{2}\right)^{-n-1}=-\frac{2nx}{\left(1+x^{2}\right)^{n+1}})
Multiply everything by
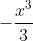
and we will have
^{n+1}})
. In conclusion we are workin g with
^{n}}dx=\int_{0}^{1}x^{2}\left(1+x^{2}\right)^{-n}dx=\frac{2^{-n}}{3}+\int_{0}^{1}\frac{2nx^{4}}{3\left(1+x^{2}\right)^{n+1}}dx)
Simply put, we have
^{n+1}}dx)
.
Now, multiply by 3
^{n+1}}dx)
^{n+1}}dx)
Now what?
Keep an eye on this term
^{n+1}}dx)
What can you do to get something like
^{n}})
?
If you can solve that step you will obtain a huge morale boost.
^{n+1}}dx=\frac{2nx^{2}}{\left(1+x^{2}\right)^{n}}\times{\left(\frac{x^{2}}{1+x^{2}}\right))
^{n}}\times{\left(\frac{x^{2}}{1+x^{2}}\right)=\frac{2nx^{2}}{\left(1+x^{2}\right)^{n}}\times\left(1-\frac{1}{1+x^{2}}\right))
Let's finish this the final stretch.
^{n}}\times\left(1-\frac{1}{1+x^{2}}\right)=\frac{2nx^{2}}{\left(1+x^{2}\right)^{n}}-\frac{2nx^{2}}{\left(1+x^{2}\right)^{n+1}}=2nI_{n}-2nI_{n+1})
Combining it all together
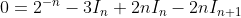
.
Rearranging we will then have
I_{n})