Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
So we all know that irrational numbers can be expressed as an infinite construction of integers in various forms.
I.e:
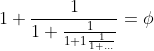
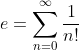
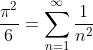
and so on.
Is it possible to construct something of an infinite series partially composed of irrational numbers, to form a rational?
i.e.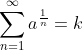
a is irrational and k is rational (this is just an example of such a way to see an infinite series composed of irrational numbers. It could be a continued fraction, infinite square roots etc.)
If this is possible, is it also possible for transcendental numbers (which I assume would be harder to do this if applicable to irrationals in the first place)
(also no trivial stuff like e-e=0, e is irrational etc)
And yes you can technically for example rearrange the Basel problem to make 6 the subject and etc. But I'm looking for an actual series.
I.e:
and so on.
Is it possible to construct something of an infinite series partially composed of irrational numbers, to form a rational?
i.e.
a is irrational and k is rational (this is just an example of such a way to see an infinite series composed of irrational numbers. It could be a continued fraction, infinite square roots etc.)
If this is possible, is it also possible for transcendental numbers (which I assume would be harder to do this if applicable to irrationals in the first place)
(also no trivial stuff like e-e=0, e is irrational etc)
And yes you can technically for example rearrange the Basel problem to make 6 the subject and etc. But I'm looking for an actual series.
Last edited:
