-
Looking for HSC notes and resources? Check out our Notes & Resources page
Roots (1 Viewer)
- Thread starter NexusRich
- Start date
- Joined
- Feb 16, 2005
- Messages
- 8,132
- Gender
- Male
- HSC
- 2006
This isn't a "shorter way" per se, but is an alternative if you're really that lazy to expand...
Let
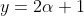
. Since 
is a root of the polynomial then
^3}{8}-2\times\dfrac{(y-1)^2}{4}+4\times\dfrac{(y-1)}{2}+7=0)
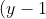^3 - 4(y-1)^2 + 16(y-1)+56=0)
Since we get same result regardless of whether we define y in terms of
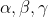
then this new equation has the roots 
.
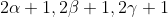
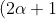Hence(2\beta+1)(2\gamma+1))
is just the product of the roots of that new equation.
By inspection of the expansion we can see that the constant term is -1- 4-16+56, or equivalently 35. The product of the roots is therefore -35.
Let
Since we get same result regardless of whether we define y in terms of
Hence
By inspection of the expansion we can see that the constant term is -1- 4-16+56, or equivalently 35. The product of the roots is therefore -35.