So I’m half way through 4u integration and I just feel so overwhelmed by all the rules, different types and methods to solve it. At the same time, I also feel like I really like doing integration (no idea if this makes sense  ) ) as it is just so interesting and satisfying when you get it right. That is why I would like to know some tips on integration, more specifically how to identify the correct method and what are all of the methods used in 4u HSC. Thank you so much in advance.
) ) as it is just so interesting and satisfying when you get it right. That is why I would like to know some tips on integration, more specifically how to identify the correct method and what are all of the methods used in 4u HSC. Thank you so much in advance.
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Tips on how to excel in Integration (1 Viewer)
- Thread starter catha230
- Start date
HeroWise
Active Member
- Joined
- Dec 8, 2017
- Messages
- 353
- Gender
- Male
- HSC
- 2020
You dont simply just 'Excel' in integration. You use Latex...
I mean, the simplest way to approach Integration would be to know the various types they can ask in HSC. They cant be too creative, but cant be too bland either. There should be a middle ground. Anyway, from doing the chapters, which one do you find more difficult. If its a culmination of them, i suggest you write down all the rules in a piece of paper and look at it everyday, till its muscle memory.
I mean, the simplest way to approach Integration would be to know the various types they can ask in HSC. They cant be too creative, but cant be too bland either. There should be a middle ground. Anyway, from doing the chapters, which one do you find more difficult. If its a culmination of them, i suggest you write down all the rules in a piece of paper and look at it everyday, till its muscle memory.
TheOnePheeph
Active Member
- Joined
- Dec 13, 2018
- Messages
- 241
- Gender
- Male
- HSC
- 2019
It all really comes from experience. Generally, the integrals you get given aren't super complicated, so the method shouldn't be too difficult to identify.So I’m half way through 4u integration and I just feel so overwhelmed by all the rules, different types and methods to solve it. At the same time, I also feel like I really like doing integration (no idea if this makes sense) ) as it is just so interesting and satisfying when you get it right. That is why I would like to know some tips on integration, more specifically how to identify the correct method and what are all of the methods used in 4u HSC. Thank you so much in advance.
Usually, as soon as you see a product of two separate 'types' of functions, you will be able to realise isntantly that IBP is the way to go (i.e. xlnx, xe^x, xsinx etc), as well as for a few other functions that are able to be reduced to easily integrated forms (lnx, arcsinx, arccosx, arctanx).
U subs are generally pretty easy to spot when you have a more complicated expression in the integral somewhere, but this more comes from experience.
Partial fraction questions are almost always exactly the same, you will simply have a rational function that you need to perform partial fraction decomposition on, in fact usually they straight up tell you that this is the method you should use.
A few more obscure techniques include using "Kings Property", which is the fact that:
This is generally a question, but it almost always contains some trigonometric expression with bounds pi/2 and 0, and the question generally tells you to make the substitution pi/2 - x. Otherwise the question may tell you to prove the more simple case where the lower bound is 0, and then give you a fairly simple integral to evaluate with it.
There is also the really rare case of making the substitution u=-x and adding this back onto the original integral to get an easily integrated function. A lot of the other ones are generally just algebraic manipulation, i.e. using trig identities. None of these should be too difficult however.
Integration is hard - unlike differentiation it's not a mechanical process: there isn't a set sequence of steps you can take that always gives you the answer. In fact, most functions don't even have antiderivatives.
The best way to get better is to just simply practice. You'll develop an intuition for what techniques are more likely to work for a certain integral.
In MX2, you'll mainly be using the following:
- -substitution
-substitution
This method can be deceptively tricky, but in the scope of MX2 you shouldn't have many problems with it.
Usually the substitution is not hard to find. For example, if you see a certain function appear several times in the integral then you might try that function as a substitution.
There are two types of substitutions you can try: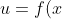) , or
, or 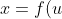) .
.
The main difference with these two is what happens with the differential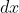 .
.
For the former, you'll have to find some function of to take out of the integrand and combine with
to take out of the integrand and combine with 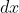 to turn into
to turn into 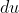 , e.g.
, e.g. 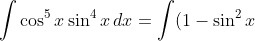^2(\sin^4x)\, (\cos x \,dx) \stackrel{u\, = \, \sin x}{=} \int (1-u^2)u^4 \, du)
For the latter you don't have to do this - the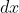 will expand into a function of
will expand into a function of 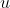 multiplied by
multiplied by 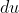 . This can give you more to work with.
. This can give you more to work with.
e.g.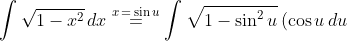)
- Integration by parts
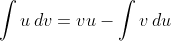
In general you want to use this on integrands that are a product of two functions - one should be easy to differentiate, and the other should be easy to integrate. Ideally these functions should not become more "complicated" after differentiation/integration.
Some examples are
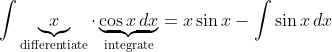
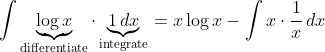
In some cases, the latter function could simply be the constant function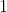 . This is quite useful for many functions, including all the inverse trig ones.
. This is quite useful for many functions, including all the inverse trig ones.
- Partial fraction decomposition
This is for integrating rational functions, where the degree of the denominator is higher than that of the numerator, and the denominator can be factorised. It's fairly straightforward, but one thing to remember is that if you have a repeated power of a factor then your decomposition needs to contain every decreasing power of that factor, e.g.
^3} = \frac{A}{x-1} + \frac{B}{(x-1)^2} + \frac{C}{(x-1)^3} )
As well as these, you can often algebraically manipulate the integrand into a form where the integration method becomes easy to see, especially if you're dealing with trig functions. So before you even start trying to integrate, see if you can play around with the integrand to make things easier.
For example, completing the square can be helpful.
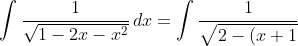^2}}\, dx=\sin^{-1}\left(\frac{x+1}{\sqrt 2}\right)+C)
The best way to get better is to just simply practice. You'll develop an intuition for what techniques are more likely to work for a certain integral.
In MX2, you'll mainly be using the following:
-
This method can be deceptively tricky, but in the scope of MX2 you shouldn't have many problems with it.
Usually the substitution is not hard to find. For example, if you see a certain function appear several times in the integral then you might try that function as a substitution.
There are two types of substitutions you can try:
The main difference with these two is what happens with the differential
For the former, you'll have to find some function of
For the latter you don't have to do this - the
e.g.
- Integration by parts
In general you want to use this on integrands that are a product of two functions - one should be easy to differentiate, and the other should be easy to integrate. Ideally these functions should not become more "complicated" after differentiation/integration.
Some examples are
In some cases, the latter function could simply be the constant function
- Partial fraction decomposition
This is for integrating rational functions, where the degree of the denominator is higher than that of the numerator, and the denominator can be factorised. It's fairly straightforward, but one thing to remember is that if you have a repeated power of a factor then your decomposition needs to contain every decreasing power of that factor, e.g.
As well as these, you can often algebraically manipulate the integrand into a form where the integration method becomes easy to see, especially if you're dealing with trig functions. So before you even start trying to integrate, see if you can play around with the integrand to make things easier.
For example, completing the square can be helpful.
