i) If one ball is chosen, there are 2 possibilities - 1 red or 1 blue
If two balls are chosen, there are 3 possibilities - both red or both blue or 1 red & 1 blue
If three balls are chosen, there are 4 possibilities - all red or all blue, or two red & 1 blue or two blue & 1 red
Thus by observing the pattern; if r balls are chosen, there is r + 1 possible colour combinations.
ii) Choosing n - r balls from n balls:
No. of selections:
![n-(n-r)]!} \\\\ = \frac {n!}{(n-r)!r!} \\\\ = \binom{n}{r}, $ as$ $ required. $ )
iii) In a particular selection, r red or r blue balls can be chosen in (r+1) ways, [from (i)]. The remaining (n-r) balls will therefore be white and can be chosen in nCr ways, [from (ii)].
So each selection or r red balls or r blue balls and (n-r) white balls can be made in (r+1)nCr ways.
The no. of red or blue balls can range from 0 to n, so the number of possible selections:
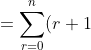 \binom{n}{r} \\\\ $Total$ $ possible $ $selections $ \\\\ = 1\binom{n}{0} + 2\binom{n}{1} + 3\binom{n}{2} + ... + (n+1)\binom{n}{n} \\\\ = 1\binom{n}{1} + 2\binom{n}{2} + 3\binom{n}{3} + ... + n\binom{n}{n} + \binom{n}{0} + \binom{n}{1} + \binom{n}{2} + ... + \binom{n}{n} \\\\ = \sum_{k=1}^{n}k\binom{n}{k} + \sum_{k=0}^{n}\binom{n}{k} \\\\ = n2^{n-1} + 2^n $ from$ $ part$ $ (b)$ $ of$ $ Question$ $ 7$ \\\\ = (n+2)2^{n-1} )