Diagrams are very helpful in these sorts of questions...

i)After finding angle ABC as shown in diagram, use the cosine rule to determine distance CA, or x.
(18)(cos83)\\x^2 &= 839.32....\\x &= 28.97... \text{ miles}\\x &\approx 29 \text{ miles} \end{align*} )
ii) The acute angle between the grey line and the black line at C must equal 67°, because it is co-interior to the 83° and 30° at B.
We can then use the sine rule to divide the 67° into the angle in the triangle, and therefore work out the bearing angle.
<a href="http://www.codecogs.com/eqnedit.php?latex=\text{Let } y = \angle ACB\\ \\ \frac{siny}{18} = \frac{sin83}{29}\\ \\ siny = \frac{18sin83}{29}\\ \\ y = 38.03....\\ \therefore \angle ACB \approx 38 \text{ degrees}\\" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\text{Let } y = \angle ACB\\ \\ \frac{siny}{18} = \frac{sin83}{29}\\ \\ siny = \frac{18sin83}{29}\\ \\ y = 38.03....\\ \therefore \angle ACB \approx 38 \text{ degrees}\\" title="\text{Let } y = \angle ACB\\ \\ \frac{siny}{18} = \frac{sin83}{29}\\ \\ siny = \frac{18sin83}{29}\\ \\ y = 38.03....\\ \therefore \angle ACB \approx 38 \text{ degrees}\\" /></a>
The true bearing of A from C is then
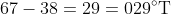
and the compass bearing is something like
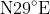
(if i recall compass bearings correctly!)


