-
Looking for HSC notes and resources? Check out our Notes & Resources page
Vector help (1 Viewer)
- Thread starter ALOZZZ
- Start date
I don't know how to do the column vector in LaTeX; so I'll use the horizontal equivalent.
Q7.
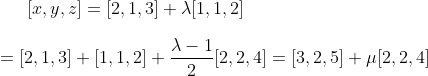
Therefore the same line.
For vector eqn of a line: you have one (any one of the infinite number of) points on the line and a direction vector, in this case [1, 1, 2] or any nonzero multiple of this vector, like 2 x [1, 1, 2] = [2, 2, 4]. This is like being able to specify the eqn of a line in your Yr-9 or Yr-10 co-ordinate geometry, given one point on the line and its direction (i.e. the gradient).
So for this particular line, its vector equation is not unique, because you can choose any one point on the line, and any equivalent direction vector, which is a portion, or a multiple, of any one direction vector. So the two different vector equations given are just 2 of the infinite number of equivalent vector equations of the line.
You could have done this question by showing the point (2, 1, 3) lies on the 2nd line (how? by finding a value of lambda-2 in line-2 that will give you the 1st point) and the point (3, 2, 5) on the 2nd line lies on the 1st line, provided these 2 points are distinct, i.e. not the same point.
Q7.
Therefore the same line.
For vector eqn of a line: you have one (any one of the infinite number of) points on the line and a direction vector, in this case [1, 1, 2] or any nonzero multiple of this vector, like 2 x [1, 1, 2] = [2, 2, 4]. This is like being able to specify the eqn of a line in your Yr-9 or Yr-10 co-ordinate geometry, given one point on the line and its direction (i.e. the gradient).
So for this particular line, its vector equation is not unique, because you can choose any one point on the line, and any equivalent direction vector, which is a portion, or a multiple, of any one direction vector. So the two different vector equations given are just 2 of the infinite number of equivalent vector equations of the line.
You could have done this question by showing the point (2, 1, 3) lies on the 2nd line (how? by finding a value of lambda-2 in line-2 that will give you the 1st point) and the point (3, 2, 5) on the 2nd line lies on the 1st line, provided these 2 points are distinct, i.e. not the same point.
Last edited:
Q6.
Can use as direction vector: [2, 5, 3] = [2, 7, 4] - [ 0, 2, 1]
So a vector eqn of the line is: [x, y, z] = [0, 2, 1] + k[2, 5, 3]
Parametric eqns: x = 2k, y = 2 + 5k, z = 1 + 3k
When y = 1, 2 + 5k = 1 ==> k = -1/5
Therefore a1 = 2k = -2/5 and a3 = 1-3/5 = 2/5
Here I've found a vector equation of the line. I then found the value of the parameter lambda corresp. to the point on it with y = 1 (there is only one such point). You can then use this value of lambda to find the corresponding value of z, or "a3".
Can use as direction vector: [2, 5, 3] = [2, 7, 4] - [ 0, 2, 1]
So a vector eqn of the line is: [x, y, z] = [0, 2, 1] + k[2, 5, 3]
Parametric eqns: x = 2k, y = 2 + 5k, z = 1 + 3k
When y = 1, 2 + 5k = 1 ==> k = -1/5
Therefore a1 = 2k = -2/5 and a3 = 1-3/5 = 2/5
Here I've found a vector equation of the line. I then found the value of the parameter lambda corresp. to the point on it with y = 1 (there is only one such point). You can then use this value of lambda to find the corresponding value of z, or "a3".
Last edited:
Q8.
You are here given the Cartesian equation of a line.
}{\frac {3}{2}} $ a line passing thru the point $ (2, \frac{1}{3}, -\frac {1}{2} ) $ with direction vector: $ [-7, \frac {5}{3}, \frac {3}{2} ] )
You can now write down a vector eqn of the line.
Here, rewrite the Cartesian eqn is a standard form. You can then read off the components of the direction vector and the co-ords of the point on the line. If you don't like fractions, you can use an equivalent direction vector like 6x[ . . . ] = [-42, 10, 9].
You are here given the Cartesian equation of a line.
You can now write down a vector eqn of the line.
Here, rewrite the Cartesian eqn is a standard form. You can then read off the components of the direction vector and the co-ords of the point on the line. If you don't like fractions, you can use an equivalent direction vector like 6x[ . . . ] = [-42, 10, 9].
Last edited:
Thank you soo much, but can you please walk me through your steps?I don't know how to do the column vector in LaTeX; so I'll use the horizontal equivalent.
Q7.
Therefore the same line.
which steps? Every one?Thank you soo much, but can you please walk me through your steps?
Yes please. btw its only for the question number 7which steps? Every one?
Question 7
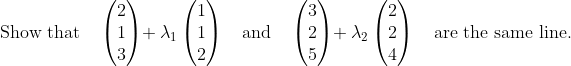
Comments and Solution #1
This question is (conceptually) the equivalent of showing that
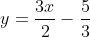
is the same as
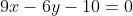 .
.
@Drongoski has taken the same approach to this 3D line as would be taken for the 2D line problem... rewriting one form of the equation into the other, involving finding a relationship between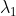 and
and 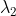 .
.
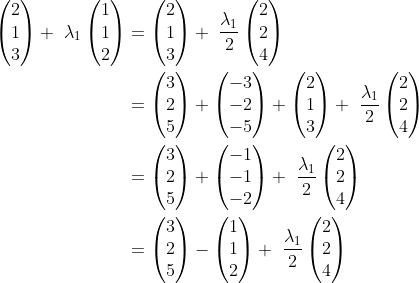
\begin{pmatrix}2\\2\\4\end{pmatrix} \\ &= \begin{pmatrix}3\\2\\5\end{pmatrix} +\ \lambda_2\begin{pmatrix}2\\2\\4\end{pmatrix} \qquad \text{where } \lambda_2 = \frac{\lambda_1 - 1}{2} \end{align*})
Solution #2(a) and (b)
A different approach is to show that the relationship between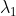 and
and 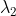 is the same for each of the three coordinate axes. That is, if
is the same for each of the three coordinate axes. That is, if
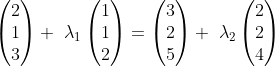
Then, in the -direction, we have
-direction, we have
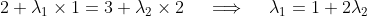
And, in the -direction, we have
-direction, we have
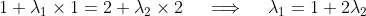
And, in the -direction, we have
-direction, we have
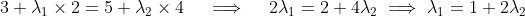
This proof could also be constructed by using the result from the -direction to get that
-direction to get that
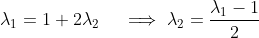
and then substitute into the second equation and show that the first results:
\begin{pmatrix}1\\1\\2\end{pmatrix} \\ &= \begin{pmatrix}3\\2\\5\end{pmatrix} +\ \lambda_1\begin{pmatrix}1\\1\\2\end{pmatrix} - \begin{pmatrix}1\\1\\2\end{pmatrix} \\ &= \begin{pmatrix}2\\1\\4\end{pmatrix} +\ \lambda_1\begin{pmatrix}1\\1\\2\end{pmatrix} \\ &= \text{ LHS} \end{align*})
Comments and Solution #1
This question is (conceptually) the equivalent of showing that
is the same as
@Drongoski has taken the same approach to this 3D line as would be taken for the 2D line problem... rewriting one form of the equation into the other, involving finding a relationship between
Solution #2(a) and (b)
A different approach is to show that the relationship between
Then, in the
And, in the
And, in the
This proof could also be constructed by using the result from the
and then substitute into the second equation and show that the first results:
Question 7
Comments and Solution #1
This question is (conceptually) the equivalent of showing that
is the same as
.
@Drongoski has taken the same approach to this 3D line as would be taken for the 2D line problem... rewriting one form of the equation into the other, involving finding a relationship betweenand
.
Solution #2(a) and (b)
A different approach is to show that the relationship betweenand
is the same for each of the three coordinate axes. That is, if
Then, in the-direction, we have
And, in the-direction, we have
And, in the-direction, we have
This proof could also be constructed by using the result from the-direction to get that
and then substitute into the second equation and show that the first results:
\begin{pmatrix}1\\1\\2\end{pmatrix} \\ &= \begin{pmatrix}3\\2\\5\end{pmatrix} +\ \lambda_1\begin{pmatrix}1\\1\\2\end{pmatrix} - \begin{pmatrix}1\\1\\2\end{pmatrix} \\ &= \begin{pmatrix}2\\1\\4\end{pmatrix} +\ \lambda_1\begin{pmatrix}1\\1\\2\end{pmatrix} \\ &= \text{ LHS} \end{align*})

