Here is my take on this question.
Let vector
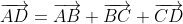
and
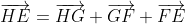
Exploit the fact that for a regular octagon suppose
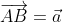
then theoretically
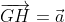
and for a regular octagon we see that
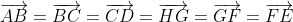
because these vectors are going in the same direction.
As a result of out first statement, we said that
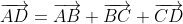
and
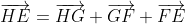
.
Using that we can say

.