I believe that in my memory this is where it comes from
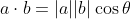
.
This comes from the angle for vectors.
There, what you do is replace

with

and then what you will have is
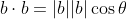
.
The interesting part is that since

lies in the same direction of

then
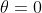
which leads to
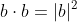
beccause
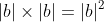
. Note this is for two vectors going in the same direction.
For vectors going in the opposite direction
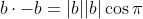
.
Vectors in this case are parallel and collinear.