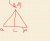
Oh i just wanted to reach the conclusion with the last paragraph quickly. I constructed that vector as an arbitrary vector that will act as a bisector. Didnt want to use the fact that its half a rhombus and in essence that is the way the complex method I was referring to would've been established. The other reason I did not put it as the form you referred to above was because i just wished to prove that the vector c was perpendicular. Didnt need any other stuff for it so didn't go with the definition you have provided above; so the proof
should be sufficient to say the very least.
It is possible to simply skip defining
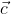
explicitly, and even if I were to do so, I would not offer an ambiguous definition of
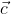
as you have done. It simply invites questions as to why that definition was chosen and whether the
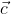
that you have defined actually has the properties that you claim. In this situation, it is odd to define
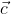
by means of a dot product as it means that
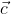
is not a unique vector as there is more than one
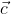
that satisfies your definition. Under your definition,
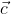
must satisfy
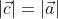
and have an angle between it and
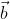
as
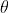
- but there are two vectors that fit these criteria and only one of them is the bisector that you seek.
It is sufficient to provide a limited defition: that
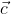
is a vector that bisects the angles between
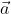
and
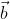
, so that the angle between
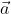
and
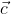
and the angle between
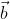
and
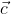
are the same (i.e.
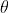
) and thus that the angle between
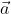
and
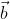
is
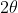
subject to the requirements that
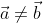
and
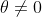
.
In other words, by simply naming
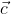
and defining it as having the properties of a bisector, your proof that the dot product
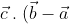 = 0)
follows quickly and without distraction. As a marker, I would have to stop and consider whether your
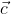
is actually valid, and the definition itself is not used for the proof in any event so it isn't actually needed.