Dragonmaster262
Unorthodox top student
Solve simultaneously:
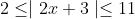
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Hint:Solve simultaneously:
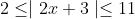
Does that count as solving simultaneously?Hint:
Solve | 2x + 3 | ≥ 2 and | 2x + 3 | ≤ 11 separately, and find the intersection of the two sets of solutions found in each case.
1. Generally by looking at the equation and finding roots, you can tell where the graph is positive/negative (roots are zero). You can test points around the root if you're not sure.Q) How do you know where the graph of a function is positive/negative or zero? When a function is negative is it said to be decreasing and vice versa?
Q) What does it mean, when it you say that a function is bounded?
Q) How do you find the horizontal asymptoe of a function? If it has any that is.
Worded answers would be suffice. There's no need to be using Latex.
So how do you tell if a function is postive, negative or zero by just looking at the function graph?1) To find where it is positive/negative/zero u sub in x values, and if the resulting f(x) value will be positive/negativ/zero. NO it DOES NOT mean it's decreasing..HOWEVER if f'(x) < 0 (the first derivative is less then zero) the the function IS decreasing as the gradient is negative
2) When a function is bounded it literally means that it has boundaries, it does not go to infinity
3) horizontal asymptotes can be found by either dividing the function (polynomial divisions) and taking the limit as x --> infinity, or by simply by looking at the leading term and its coefficients...
1) When it is ABOVE the x axis it is positive, when it is BELOW the x axis it is negative, when it TOUCHES the x axis it is zeroSo how do you tell if a function is postive, negative or zero by just looking at the function graph?
Is it still bounded if it has discontinuities in between but still continues along the x and y axes?
4) If a function is at a discontinuity on the x axis, is it said to be constant?
dont get any of those questionsSo how do you tell if a function is postive, negative or zero by just looking at the function graph?
Is it still bounded if it has discontinuities in between but still continues along the x and y axes?
4) If a function is at a discontinuity on the x axis, is it said to be constant?
This is why numeracy alone isn't enough to bypass maths.dont get any of those questions
lolThis is why numeracy alone isn't enough to bypass maths.
uh what?This is why numeracy alone isn't enough to bypass maths.
Thanks GUESSSSSS.
I never said he was dumb. I was just cracking a joke. Sorry, if I offended you Tim.uh what?
You don't know how smart tim is, he gotta be one of the top 09 maths wizards here along with lolokay, jetblack and gurmies.
increasing -> the graph is heading right and upWait, there's one question I forgot to ask. How do you tell if a function is increasing/decreasing by just looking at its graph?
Thanks Namu. Finally, this thread is over.increasing -> the graph is heading right and up
decreasing -> the graph is heading right and down

