-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Trigonometry Question: (1 Viewer)
- Thread starter Divinity_
- Start date
gurmies
Drover
Or t-method, where t = tan(x/2). If this means nothing to you, I can post solution.
Official
Bring it on
Equating coefficients
Substituting values back in
Then you solve this simplified equation for answer.
annabackwards
<3 Prophet 9
I was just about to suggest this methodor you can do it this way:
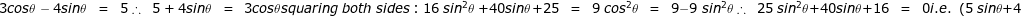^{2} \ =\ 0\\ \\ \therefore \ \ 5\ sin\theta +4\ =\ 0\ \ \Rightarrow \ \ sin\theta \ =\ -0.8\\ \\ \therefore \ \ \theta \ =\ -53^{\circ} \ 8{}'\ \ \ or\ \ \ -126^{\circ}\ 52{}')
It is often easier and more intuitive but is not widely adopted.I was just about to suggest this method
philly2000
New Member
- Joined
- Feb 11, 2009
- Messages
- 29
- Gender
- Male
- HSC
- 2010
wow just learnt a new method, thanks drongoski !
Official
Bring it on
lol this is such a good method! You dont have to go through all that random crap lollzzor you can do it this way:
Is this answer right ??
Aquawhite
Retiring
Whatever you can do to make it simplier... by squaring it makes things so much more simple. I really like that squaring method (very simple and just obvious).
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
remember squaring can add false solutions
annabackwards
<3 Prophet 9
How so? It has always worked for me...remember squaring can add false solutions
K
khorne
Guest
Well
x = 5
x^2 = 25
sqrt both sides
therefore
x = +/- 5
You get two solutions when you originally had one.
x = 5
x^2 = 25
sqrt both sides
therefore
x = +/- 5
You get two solutions when you originally had one.
untouchablecuz
Active Member
- Joined
- Mar 25, 2008
- Messages
- 1,693
- Gender
- Male
- HSC
- 2009
consider
sin x + cos x = 1, 0<=x<=2pi
squaring both sides
sin^2x +2sinxcosx + cos^2x = 1
1 + sin2x = 1
sin2x = 0, 0<=2x<=2pi
solutions: x = 0, pi/2, pi, 3pi/2, 2pi
sub in x = 0, pi/2, 2pi into sin x + cos x = 1 and the equation is satisified
sub in x = pi, 3pi/2 into sin x + cos x and we get -1 =/= 1
hence pi and 3pi/2 are not solutions and were included when squaring
sin x + cos x = 1, 0<=x<=2pi
squaring both sides
sin^2x +2sinxcosx + cos^2x = 1
1 + sin2x = 1
sin2x = 0, 0<=2x<=2pi
solutions: x = 0, pi/2, pi, 3pi/2, 2pi
sub in x = 0, pi/2, 2pi into sin x + cos x = 1 and the equation is satisified
sub in x = pi, 3pi/2 into sin x + cos x and we get -1 =/= 1
hence pi and 3pi/2 are not solutions and were included when squaring
gurmies
Drover
Exactly. Test when squaring.consider
sin x + cos x = 1, 0<=x<=2pi
squaring both sides
sin^2x +2sinxcosx + cos^2x = 1
1 + sin2x = 1
sin2x = 0, 0<=2x<=2pi
solutions: x = 0, pi/2, pi, 3pi/2, 2pi
sub in x = 0, pi/2, 2pi into sin x + cos x = 1 and the equation is satisified
sub in x = pi, 3pi/2 into sin x + cos x and we get -1 =/= 1
hence pi and 3pi/2 are not solutions and were included when squaring
annabackwards
<3 Prophet 9
Ah, noted ^^Exactly. Test when squaring.
Caution using the quadratic eqn methodAh, noted ^^
I was going to post a cautionary note about the method I used:
1) don't use it if reqd to do using auxillary angle or t-formula method
2) when you square: LHS = RHS you get new eqn: LHS2 = RHS2
The solutions to this new eqn include those for LHS = -RHS.
So you have to test for and to exclude these.
I think it is still a lot shorter and easier in general.
Timothy.Siu
Prophet 9
5cos(@+tan-1(4/3))=5Solve:
3cos theta - 4sin theta = 5 for -pi <= theta <= pi
cos(@+tan-1(4/3))=1
@+tan-1(4/3)=0
@=-tan-1(4/3)
drongonski, ur other solution is wrong (i think)
because 3cos -126 would be negative (not in the positive quadrants), and 4sin (anything) can't be greater than 4
Last edited:
Dumbledore
Member
- Joined
- Sep 11, 2008
- Messages
- 290
- Gender
- Male
- HSC
- 2009
just wondering when using the acos(x)+bsin(x)=Rsin(x+@)
can u just say R=sqrt(a^2+b^2) and @=arctan(b/a)
or do u have to expand Rsin(x+@) and equate co efficients?
can u just say R=sqrt(a^2+b^2) and @=arctan(b/a)
or do u have to expand Rsin(x+@) and equate co efficients?
