shuning
Member
- Joined
- Aug 23, 2008
- Messages
- 654
- Gender
- Male
- HSC
- 2009
When ^n ) is expanded in increasing powers of x, it is found that the coefficients of
is expanded in increasing powers of x, it is found that the coefficients of 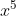 and
and 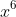 have the same value. find the value of n and show that the 2 coefficients mentioned are greater than all other coefficients in the expansion
have the same value. find the value of n and show that the 2 coefficients mentioned are greater than all other coefficients in the expansion
i got n =23 ( would be nice if u can check for me if i got correct or not... cuz i dont have the answers. )
But how do i do the 2nd part?
i got n =23 ( would be nice if u can check for me if i got correct or not... cuz i dont have the answers. )
But how do i do the 2nd part?
