Riproot
Addiction Psychiatrist
- Joined
- Nov 10, 2009
- Messages
- 8,226
- Gender
- Male
- HSC
- 2011
- Uni Grad
- 2017
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
y=ln x, dy/dx= 1/xFind the equation of the tangent to the curve y = ln x such that the tangent passes through the origin.
Hence show that
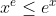
it is true for x=0y=ln x, dy/dx= 1/x
as the tangent passes through the origin, the tangent has an equation in the form
y=mx. But m=dy/dx,
. ' . solving simultaneously
ln x=1/x * x
ln x=1
x=e
when x=e, y=1
using (e,1) , m=1/e
y=x/e
I was wondering if a proof such as this is valid:
x^e is less than or equal to e^x
when x^e = e^x,
by inspection, x=e
when x approaches positive infinity, e^x>x^e
when x approaches 0, e^x>x^e
hence x^e is less than or equal to e^x?
remember its an inequalityat x=0,
(0)^e = e^0
0=1
???
I've seen that Q before. Probably the 2009 CSSA.Yes I'm starting this thingy again because yeah... the old one is gone.
I'll start with a simple one on maxima/minima:
View attachment 22464
thats been put up before by trebla i thinkI've seen that Q before. Probably the 2009 CSSA.
Here's an interesting Q: Prove 3/4+5/36+7/144+9/400+11/900+...= 1
That was a Q9 HSC question a couple of years ago. Completely stupid and I hated doing it for revision lol.Trebla said:Find the equation of the tangent to the curve y = ln x such that the tangent passes through the origin.
Hence show that...
Get out. *points at door*AC = 2root(100-x^2)
Therefore A triangle = 1/2 x 2root(100-x^2) x (10+x)
Differentiate it using the product rule. Equate to 0 and solve for x. Determine max point
Use shift cos to prove the two 60 degrees and then use angle sum.
someone post next question
2U thread? What am I supposed to say? Inverse cosine function/Inverse cos? People wont know what you're on about, except you and everyone who has done inverse functions of courseGet out. *points at door*
I doubt most students in year 9 would've learnt this term. You must have a good teacher.I learned to call it inverse cos when i was in year 9. If they don't know, they're retarded.
Your last statement was also offensive, so, I'd say we're about even.I doubt most students in year 9 would've learnt this term. You must have a good teacher.
Your second statement will be offensive to a lot of people. So please, get off your high horse

