Here's the answer to your first query:
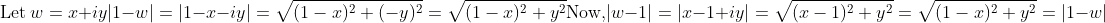
You can also think about it using vectors, or you can simply factorise out a -1 and then you get the desired result.
Give me a few minutes and I'll do the other parts.
<a href="http://www.codecogs.com/eqnedit.php?latex=\\ \textrm{Let}~z=r_1cis\theta_1~\textrm{and}~w=r_2cis\theta_2\\ \frac{z}{w}\\ =\frac{r_1cis\theta_1}{r_2cis\theta_2}\\ =\frac{r_1}{r_2}cis (\theta_1-\theta_2)\\ ~\\ \textrm{Hence,} \left | \frac{z}{w}\right |=\frac{r_1}{r_2}=\frac{|z_1|}{|z_2|}\\ \therefore \textrm{If}~z=\frac{1}{1-w},~\textrm{then}~|z|=\left|\frac{1}{1-w}\right|=\frac{1}{|1-w|}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ \textrm{Let}~z=r_1cis\theta_1~\textrm{and}~w=r_2cis\theta_2\\ \frac{z}{w}\\ =\frac{r_1cis\theta_1}{r_2cis\theta_2}\\ =\frac{r_1}{r_2}cis (\theta_1-\theta_2)\\ ~\\ \textrm{Hence,} \left | \frac{z}{w}\right |=\frac{r_1}{r_2}=\frac{|z_1|}{|z_2|}\\ \therefore \textrm{If}~z=\frac{1}{1-w},~\textrm{then}~|z|=\left|\frac{1}{1-w}\right|=\frac{1}{|1-w|}" title="\\ \textrm{Let}~z=r_1cis\theta_1~\textrm{and}~w=r_2cis\theta_2\\ \frac{z}{w}\\ =\frac{r_1cis\theta_1}{r_2cis\theta_2}\\ =\frac{r_1}{r_2}cis (\theta_1-\theta_2)\\ ~\\ \textrm{Hence,} \left | \frac{z}{w}\right |=\frac{r_1}{r_2}=\frac{|z_1|}{|z_2|}\\ \therefore \textrm{If}~z=\frac{1}{1-w},~\textrm{then}~|z|=\left|\frac{1}{1-w}\right|=\frac{1}{|1-w|}" /></a>
