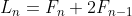HSC 2012 MX2 Marathon (archive) (2 Viewers)

Carrotsticks · Mar 2, 2012

Re: 2012 HSC MX2 Marathon

Nooblet94 said:
Here's an interesting question I just did:

Generate a formula for the nth term of the Fibonacci series (1,1,2,3...)
Hence, find a formula for the nth term of the Lucas series (1,3,4,7...)given that $L_n=F_n+2F_{n-1}$

Very nice question.

SpiralFlex · Mar 2, 2012

Re: 2012 HSC MX2 Marathon

$F_{n+2}=F_{n+1}+F_{n}$

$$Let F_{n}=a^n$

Forming a polynomial

$a^{n+2}=a^{n+1}+a^n$

$a^2-a-1=0$

$a=\psi, \varphi$

$\therefore F_{n}=\varphi^n$

System of linear equations,

$F_{n}=A \varphi^n +B\psi^n=1$

Since we know,

$F_{0}=A+B=1$

$F_{1}=A \varphi +B\psi=1$

Solve and arrange.

$F_{n}=\frac{\varphi^n - \psi^n}{\sqrt{5}}$

Now you can deduce Lucas my neighbour.

bleakarcher · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

SpiralFlex said:
$F_{n+2}=F_{n+1}+F_{n}$

$$Let F_{n}=a^n$

Forming a polynomial

$a^{n+2}=a^{n+1}+a^n$

$a^2-a-1=0$

$a=\psi, \varphi$

$\therefore F_{n}=\varphi^n$

System of linear equations,

$F_{n}=A \varphi^n +B\psi^n=1$

Since we know,

$F_{0}=A+B=1$

$F_{1}=A \varphi +B\psi=1$

Solve and arrange.

$F_{n}=\frac{\varphi^n - \psi^n}{\sqrt{5}}$

Now you can deduce Lucas my neighbour.

Spiral, you have used the symbol phi which represents the golden ratio. But what does the other symbol represent?

SpiralFlex · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

Kekekekekeke

$\psi=\frac{1-\sqrt{5}}{2}=1-\varphi=-\frac{1}{\varphi}$

bleakarcher · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

SpiralFlex said:
Kekekekekeke

$\psi=\frac{1-\sqrt{5}}{2}=1-\varphi=-\frac{1}{\varphi}$

Interesting, thanks.

largarithmic · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

A beautiful question for those who have an idea what modular arithmetic is (basically you reduce every number to its remainder when divided by a number, e.g. 13 becomes 3 modulo 5, 17 becomes 5 modulo 6. Its easy to check that if say A reduces to A', and B reduces to B', then A+B reduces to A'+B' or perhaps whatever that reduces to):

Prove that for every positive integer, there exists a Fibonacci number which is divisible by that integer.

Carrotsticks · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

largarithmic said:
A beautiful question for those who have an idea what modular arithmetic is (basically you reduce every number to its remainder when divided by a number, e.g. 13 becomes 3 modulo 5, 17 becomes 5 modulo 6. Its easy to check that if say A reduces to A', and B reduces to B', then A+B reduces to A'+B' or perhaps whatever that reduces to):

Prove that for every positive integer, there exists a Fibonacci number which is divisible by that integer.

Larg, why must u post interesting questions.just as i am about to sleep? Will try.tmr.during.work.

kingkong123 · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

<a href="http://www.codecogs.com/eqnedit.php?latex=\\\textup{A relation is defined implicitly by: }x^{2}@plus;xy-2y^{2}=0.\textup{ Show that }\frac{dy}{dx}\textup{ has only two possible values: 1 and -}\frac{1}{2}. \\\textup{ Hence or otherwise, sketch the relation.}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\\textup{A relation is defined implicitly by: }x^{2}+xy-2y^{2}=0.\textup{ Show that }\frac{dy}{dx}\textup{ has only two possible values: 1 and -}\frac{1}{2}. \\\textup{ Hence or otherwise, sketch the relation.}" title="\\\textup{A relation is defined implicitly by: }x^{2}+xy-2y^{2}=0.\textup{ Show that }\frac{dy}{dx}\textup{ has only two possible values: 1 and -}\frac{1}{2}. \\\textup{ Hence or otherwise, sketch the relation.}" /></a>

bleakarcher · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

SpiralFlex said:
$F_{n+2}=F_{n+1}+F_{n}$

$$Let F_{n}=a^n$

Forming a polynomial

$a^{n+2}=a^{n+1}+a^n$

$a^2-a-1=0$

$a=\psi, \varphi$

$\therefore F_{n}=\varphi^n$

System of linear equations,

$F_{n}=A \varphi^n +B\psi^n=1$

Since we know,

$F_{0}=A+B=1$

$F_{1}=A \varphi +B\psi=1$

Solve and arrange.

$F_{n}=\frac{\varphi^n - \psi^n}{\sqrt{5}}$

Now you can deduce Lucas my neighbour.

Spiral, where did you get the expression after you wrote system of linear equations from?

Drongoski · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

kingkong123 said:
$\\\textup{A relation is defined implicitly by: }x^{2}+xy-2y^{2}=0.\textup{ Show that }\frac{dy}{dx}\textup{ has only two possible values: 1 and -}\frac{1}{2}. \\\textup{ Hence or otherwise, sketch the relation.}$

$x^2+xy-2y^2 = 0 \implies 2x + [xy'+y] - 2\times2yy' = 0 \implies y' = \frac {dy}{dx} = \frac {2x+y}{4y-x}$

$x^2+xy-2y^2 = 0 \implies (x+2y)(x-y) = 0 \implies y=x,-\frac{1}{2}x$

By substituting each case for y, we get y' = 1 and -0.5 resp.

Nooblet94 · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

<a href="http://www.codecogs.com/eqnedit.php?latex=\\ x^2@plus;xy-2y^2=0\\ (x@plus;\frac{1}{2}y)^2-\frac{9}{4}y^2=0\\ (x@plus;2y)(x-y)=0~~~~\Rightarrow y=x$ or $y=-\frac{1}{2}x\\ ~\\ $Differentiating both functions we get$\\ \frac{dy}{dx}=1$ or $\frac{dy}{dx}=-\frac{1}{2}\\ ~\\ $Hence, the graph of the function is two straight lines intersecting at the origin$" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ x^2+xy-2y^2=0\\ (x+\frac{1}{2}y)^2-\frac{9}{4}y^2=0\\ (x+2y)(x-y)=0~~~~\Rightarrow y=x$ or $y=-\frac{1}{2}x\\ ~\\ $Differentiating both functions we get$\\ \frac{dy}{dx}=1$ or $\frac{dy}{dx}=-\frac{1}{2}\\ ~\\ $Hence, the graph of the function is two straight lines intersecting at the origin$" title="\\ x^2+xy-2y^2=0\\ (x+\frac{1}{2}y)^2-\frac{9}{4}y^2=0\\ (x+2y)(x-y)=0~~~~\Rightarrow y=x$ or $y=-\frac{1}{2}x\\ ~\\ $Differentiating both functions we get$\\ \frac{dy}{dx}=1$ or $\frac{dy}{dx}=-\frac{1}{2}\\ ~\\ $Hence, the graph of the function is two straight lines intersecting at the origin$" /></a>

kingkong123 · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

<a href="http://www.codecogs.com/eqnedit.php?latex=\\\textup{Sketch the following locus of z on an Argand diagram. }\\\left | z @plus;2i \right |=Re(z)@plus;2i" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\\textup{Sketch the following locus of z on an Argand diagram. }\\\left | z +2i \right |=Re(z)+2i" title="\\\textup{Sketch the following locus of z on an Argand diagram. }\\\left | z +2i \right |=Re(z)+2i" /></a>

nightweaver066 · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

kingkong123 said:
<a href="http://www.codecogs.com/eqnedit.php?latex=\\\textup{Sketch the following locus of z on an Argand diagram. }\\\left | z @plus;2i \right |=Re(z)@plus;2i" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\\textup{Sketch the following locus of z on an Argand diagram. }\\\left | z +2i \right |=Re(z)+2i" title="\\\textup{Sketch the following locus of z on an Argand diagram. }\\\left | z +2i \right |=Re(z)+2i" /></a>

How can a modulus result in an imaginary number? lol..

SpiralFlex · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

Wut?^

Think twas a typo.

bleakarcher said:
Spiral, where did you get the expression after you wrote system of linear equations from?

Substituted the F0, F1

bleakarcher · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

SpiralFlex said:
$F_{n+2}=F_{n+1}+F_{n}$

$$Let F_{n}=a^n$

Forming a polynomial

$a^{n+2}=a^{n+1}+a^n$

$a^2-a-1=0$

$a=\psi, \varphi$

$\therefore F_{n}=\varphi^n$

System of linear equations,

$F_{n}=A \varphi^n +B\psi^n=1$

Since we know,

$F_{0}=A+B=1$

$F_{1}=A \varphi +B\psi=1$

Solve and arrange.

$F_{n}=\frac{\varphi^n - \psi^n}{\sqrt{5}}$

Now you can deduce Lucas my neighbour.

Why is it that when I sub n=0 into F(n) I get 1/sqrt(5) when it is meant to be one?

kingkong123 · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

nightweaver066 said:
How can a modulus result in an imaginary number? lol..

trueeee. there was a typo in the exercise. i think it should be Re(z) + 2 not 2i. In that case it will be a parabola, focal length 1, vertex (-1,-2) , concave up. right?

cutemouse · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

A bit of several variables calculus...

(i) Use the method of Lagrange multipliers, or otherwise, to find the maximum value of f(x,y)=4xy on the ellipse x^2 + 4y^2=4.

(ii) Give a geometrical interpretation of the result in (i).

Aesytic · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

kingkong123 said:
trueeee. there was a typo in the exercise. i think it should be Re(z) + 2 not 2i. In that case it will be a parabola, focal length 1, vertex (-1,-2) , concave up. right?

mine ended up being a sideways parabola, so i had one that was "concave right"

D94 · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

Aesytic said:
mine ended up being a sideways parabola, so i had one that was "concave right"

This is right.

Trebla · Mar 3, 2012

Re: 2012 HSC MX2 Marathon

Another reminder that this thread is intended for HSC students. If you want to post some uni maths questions, go to the extracurricular topics forum.

HSC 2012 MX2 Marathon (archive) (2 Viewers)

Retired

Well-Known Member

Active Member

Well-Known Member

Active Member

Member

Retired

Member

Active Member

Well-Known Member

Premium Member

Member

Well-Known Member

Well-Known Member

Active Member

Member

Account Closed

Member

New Member

Administrator

Users Who Are Viewing This Thread (Users: 0, Guests: 2)