-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Probability Question, need help with a logial way. (1 Viewer)
- Thread starter uniquee
- Start date
Fus Ro Dah
Member
- Joined
- Dec 16, 2011
- Messages
- 248
- Gender
- Male
- HSC
- 2013
Let's look at all the ways we can get an even total:
- Odd + Odd = Even.
- Even + Even = Even
- Even + Odd = Odd + Even = Odd.
So this makes 2/3 of all cases, since we have the same number of odd (1,3,5) as we do even (2,4,6).
So we have:
There are 6 x 6 combinations in total (First die has 6 options, second also has 6) so there are 36 options in total. However, since we have two die, we must divide by 2. This is because suppose Die #1 gets a 3 and Die #2 gets a 6. This would be the same as Die #1 getting a 6 and Die #2 gets a 3.
So we now have 18 combinations in total. As seen above, 2/3 of them are even.
So therefore the number of combinations yielding even is 18 x 2/3 = 12.
Now we must consider the totals greater than 7 that are ODD (since we have already counted even ones).
Only possible combinations are:
- 3 + 6 = 9
- 4 + 5 = 9
- 5 + 6 = 11
Adding another 3 cases.
So therefore total probability of getting a total that is EITHER even or greater than 7 is:
(12+3)/18 = 15/18 = 83.333%
- Odd + Odd = Even.
- Even + Even = Even
- Even + Odd = Odd + Even = Odd.
So this makes 2/3 of all cases, since we have the same number of odd (1,3,5) as we do even (2,4,6).
So we have:
There are 6 x 6 combinations in total (First die has 6 options, second also has 6) so there are 36 options in total. However, since we have two die, we must divide by 2. This is because suppose Die #1 gets a 3 and Die #2 gets a 6. This would be the same as Die #1 getting a 6 and Die #2 gets a 3.
So we now have 18 combinations in total. As seen above, 2/3 of them are even.
So therefore the number of combinations yielding even is 18 x 2/3 = 12.
Now we must consider the totals greater than 7 that are ODD (since we have already counted even ones).
Only possible combinations are:
- 3 + 6 = 9
- 4 + 5 = 9
- 5 + 6 = 11
Adding another 3 cases.
So therefore total probability of getting a total that is EITHER even or greater than 7 is:
(12+3)/18 = 15/18 = 83.333%
uniquee
reps2g is a stalker
- Joined
- Sep 6, 2011
- Messages
- 236
- Gender
- Male
- HSC
- 2012
I think that's the wrong answer, because it's 2/3 which is 66.666667%Let's look at all the ways we can get an even total:
- Odd + Odd = Even.
- Even + Even = Even
- Even + Odd = Odd + Even = Odd.
So this makes 2/3 of all cases, since we have the same number of odd (1,3,5) as we do even (2,4,6).
So we have:
There are 6 x 6 combinations in total (First die has 6 options, second also has 6) so there are 36 options in total. However, since we have two die, we must divide by 2. This is because suppose Die #1 gets a 3 and Die #2 gets a 6. This would be the same as Die #1 getting a 6 and Die #2 gets a 3.
So we now have 18 combinations in total. As seen above, 2/3 of them are even.
So therefore the number of combinations yielding even is 18 x 2/3 = 12.
Now we must consider the totals greater than 7 that are ODD (since we have already counted even ones).
Only possible combinations are:
- 3 + 6 = 9
- 4 + 5 = 9
- 5 + 6 = 11
Adding another 3 cases.
So therefore total probability of getting a total that is EITHER even or greater than 7 is:
(12+3)/18 = 15/18 = 83.333%
I think I may know how to do it now, it's just [18/36 + 15/36] - 9/36
which = 2/3
Thanks though.
Fus Ro Dah
Member
- Joined
- Dec 16, 2011
- Messages
- 248
- Gender
- Male
- HSC
- 2013
From where did you get this question and its answer?I think that's the wrong answer, because it's 2/3 which is 66.666667%
I think I may know how to do it now, it's just [18/36 + 15/36] - 9/36
which = 2/3
Thanks though.
Because the "Even totals" already amount to 2/3 of the total cases, let alone including those that exceed 7.
uniquee
reps2g is a stalker
- Joined
- Sep 6, 2011
- Messages
- 236
- Gender
- Male
- HSC
- 2012
I got this question from 3u book 1 by Jones & couchmanFrom where did you get this question and its answer?
Because the "Even totals" already amount to 2/3 of the total cases, let alone including those that exceed 7.
fortune_cookie
Banned
- Joined
- May 18, 2012
- Messages
- 193
- Gender
- Undisclosed
- HSC
- N/A
Just draw up a table
"Dice 1" on the top , "Dice 2" on the side
Write out all the possible outcomes (1 through 6) on the edges of the table, then add the outcomes on the edges of the table to full in the table. Then you can just highlight the values in the tables that fit the condition.
It may seem tedious but it really isn't that bad. It only takes like 1 minute to draw it up. Also, they will usually have two or three parts to a probability question. Once you do the work for part (i) , you have done the work for all the other parts as well.
"Dice 1" on the top , "Dice 2" on the side
Write out all the possible outcomes (1 through 6) on the edges of the table, then add the outcomes on the edges of the table to full in the table. Then you can just highlight the values in the tables that fit the condition.
It may seem tedious but it really isn't that bad. It only takes like 1 minute to draw it up. Also, they will usually have two or three parts to a probability question. Once you do the work for part (i) , you have done the work for all the other parts as well.
fortune_cookie
Banned
- Joined
- May 18, 2012
- Messages
- 193
- Gender
- Undisclosed
- HSC
- N/A
Answer = 30/36= 5/6
Purely from a table, done in 1 minute without trying to be fancy and make little errors by being a smartass.
Purely from a table, done in 1 minute without trying to be fancy and make little errors by being a smartass.
uniquee
reps2g is a stalker
- Joined
- Sep 6, 2011
- Messages
- 236
- Gender
- Male
- HSC
- 2012
The answer is 2/3 what i got lol..Answer = 30/36= 5/6
Purely from a table, done in 1 minute without trying to be fancy and make little errors by being a smartass.
Fus Ro Dah
Member
- Joined
- Dec 16, 2011
- Messages
- 248
- Gender
- Male
- HSC
- 2013
I have made a silly error.
Suppose we have a set of N arbitrary numbers and added any two elements of the set, then the probability of having an even total approaches 2/3 as N --> infinity.
However, this is not applicable to this problem because we are taking the sum of the elements of the Cartesian Product {1,2,3,4,5,6} X {1,2,3,4,5,6}, which does not yield an arbitrary result.
Suppose we have a set of N arbitrary numbers and added any two elements of the set, then the probability of having an even total approaches 2/3 as N --> infinity.
However, this is not applicable to this problem because we are taking the sum of the elements of the Cartesian Product {1,2,3,4,5,6} X {1,2,3,4,5,6}, which does not yield an arbitrary result.
RealiseNothing
what is that?It is Cowpea
EDIT: The actual answer is the first post of the next page.
Rolling a sum of greater than 7 or even means you can't roll a 3, 5, or 7.
You can roll a 3 in 2 different ways (2,1)(1,2).
You can roll a 5 in 4 different ways (2,3)(3,2)(1,4)(4,1).
You can roll a 7 in 6 different ways (1,6)(6,1)(5,2)(2,5)(4,3)(3,4).
The total possibilities is 36.
So

Rolling a sum of greater than 7 or even means you can't roll a 3, 5, or 7.
You can roll a 3 in 2 different ways (2,1)(1,2).
You can roll a 5 in 4 different ways (2,3)(3,2)(1,4)(4,1).
You can roll a 7 in 6 different ways (1,6)(6,1)(5,2)(2,5)(4,3)(3,4).
The total possibilities is 36.
So
Last edited:
uniquee
reps2g is a stalker
- Joined
- Sep 6, 2011
- Messages
- 236
- Gender
- Male
- HSC
- 2012
Rolling a sum of greater than 7 or even means you can't roll a 3, 5, or 7.
You can roll a 3 in 2 different ways (2,1)(1,2).
You can roll a 5 in 4 different ways (2,2)(2,2)(1,3)(3,1).
You can roll a 7 in 6 different ways (1,6)(6,1)(5,2)(2,5)(4,3)(3,4).
The total possibilities is 36.
So

wowww, that's one logical way of thinking about the questions & thnkas!
fortune_cookie
Banned
- Joined
- May 18, 2012
- Messages
- 193
- Gender
- Undisclosed
- HSC
- N/A
?Rolling a sum of greater than 7 or even means you can't roll a 3, 5, or 7.
You can roll a 3 in 2 different ways (2,1)(1,2).
You can roll a 5 in 4 different ways (2,2)(2,2)(1,3)(3,1).
You can roll a 7 in 6 different ways (1,6)(6,1)(5,2)(2,5)(4,3)(3,4).
The total possibilities is 36.
So

RealiseNothing
what is that?It is Cowpea
Fixed.
RealiseNothing
what is that?It is Cowpea
"Even totals" amount to 1/2 actually.From where did you get this question and its answer?
Because the "Even totals" already amount to 2/3 of the total cases, let alone including those that exceed 7.
The possibility of the sum being even is equal to the possbility of the sum being odd.
Edit: Wait, it should be 2/3, but that doesn't work.
Edit #2: Had another look, and it should be 1/2. I'm not even sure what is happening anymore.
Last edited:
RealiseNothing
what is that?It is Cowpea
Ok I got it, posting up a new solution, let's hope this is actually right.
RealiseNothing
what is that?It is Cowpea
The total possibilites is actually 42. This is because we have 6x6 ways of rolling dice, but we aren't actually counting the extra 6 rolls where we roll the same number on each dice.
Since we don't want to roll a 3, 5, or 7, we add all these up.
We know that a 3 is rolled in 2 ways, a 5 in 4 ways, and a 7 in 6 ways. Hence the amount of ways we roll a 3, 5, or 7 is 12.
Hence there is a chance we will roll a sum of 3, 5, or 7.
chance we will roll a sum of 3, 5, or 7.
Subtract this from one to get the chance that we roll evens or greater than 7:
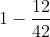


lol.
Since we don't want to roll a 3, 5, or 7, we add all these up.
We know that a 3 is rolled in 2 ways, a 5 in 4 ways, and a 7 in 6 ways. Hence the amount of ways we roll a 3, 5, or 7 is 12.
Hence there is a
Subtract this from one to get the chance that we roll evens or greater than 7:
lol.
uniquee
reps2g is a stalker
- Joined
- Sep 6, 2011
- Messages
- 236
- Gender
- Male
- HSC
- 2012
LOL..The total possibilites is actually 42. This is because we have 6x6 ways of rolling dice, but we aren't actually counting the extra 6 rolls where we roll the same number on each dice.
Since we don't want to roll a 3, 5, or 7, we add all these up.
We know that a 3 is rolled in 2 ways, a 5 in 4 ways, and a 7 in 6 ways. Hence the amount of ways we roll a 3, 5, or 7 is 12.
Hence there is achance we will roll a sum of 3, 5, or 7.
Subtract this from one to get the chance that we roll evens or greater than 7:
lol.
How is this 2u maths question confusing everyone?
it's 18/36 (all even) + 15/36 (numbers > 7) = 11/12
Then you must do - 9/36 as there are 9 numbers in > 7 which is also an even so you must subtract.
therefore it's 18/36+15/36 = 11/12 - 9/36
which is 2/3 which is the answer.
Fus Ro Dah
Member
- Joined
- Dec 16, 2011
- Messages
- 248
- Gender
- Male
- HSC
- 2013
Because most of us are thinking too deeply, having the burden of knowledge, so things get over-complicated unnecessarily.
RealiseNothing
what is that?It is Cowpea
The answer isLOL..
How is this 2u maths question confusing everyone?
it's 18/36 (all even) + 15/36 (numbers > 7) = 11/12
Then you must do - 9/36 as there are 9 numbers in > 7 which is also an even so you must subtract.
therefore it's 18/36+15/36 = 11/12 - 9/36
which is 2/3 which is the answer.
uniquee
reps2g is a stalker
- Joined
- Sep 6, 2011
- Messages
- 236
- Gender
- Male
- HSC
- 2012
it's 2/3 lol..The answer is
what maths do you do?
