AbsoluteValue
Member
A and B have (n+1) and n fair coins respectively and they toss their coins simultaneously.
a) Show that the probability that B gets r heads is given by:
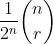
b) Hence, find the probability that A will obtain k more heads than B, where:
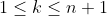
c) Show that the probability that A will obtain more heads than B is:

Probability is arguably the hardest topic in 4 unit I really need the solution to this asap.
I really need the solution to this asap.
a) Show that the probability that B gets r heads is given by:
b) Hence, find the probability that A will obtain k more heads than B, where:
c) Show that the probability that A will obtain more heads than B is:
Probability is arguably the hardest topic in 4 unit
