RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
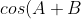=cosAcosB-sinAsinB)
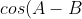=cosAcosB+sinAsinB)
Subtracting the two gives:
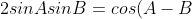+cos(A+B))
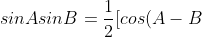+cos(A+B)])
Using this on each term in the series gives:
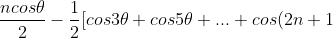\theta])
Now consider:
}{cis^2\theta-1})
Taking the real part of this gives the sum of the cosines we need, so since I cbf evaluating the real part of this, your series is equal to:
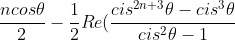)
First method I used was:Nice work guys,
 + \sin (2\theta)\sin(3\theta) + \dots + \sin(n\theta) \sin((n+1)\theta) )
Subtracting the two gives:
Using this on each term in the series gives:
Now consider:
Taking the real part of this gives the sum of the cosines we need, so since I cbf evaluating the real part of this, your series is equal to:

