RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
Let the sequence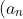) be written as:
be written as:
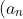=a_0+a_1+a_2+...+a_{n-1}+a_n)
Now there exists some real number such that:
such that:
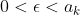 for some
for some 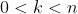
Hence we can deduce that:
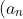 > (n-1)\epsilon)
Now as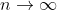 we get
we get 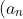 > \lim_{n \to \infty} (n-1)\epsilon)
Hence there exists a sequence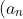) such that the limit as
such that the limit as 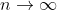 dominates
dominates 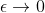 , which means
, which means 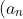 \to \infty) and it does not converge.
and it does not converge.
This will occur in a situation where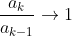 as
as 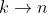
I'm not sure if this explanation is correct for the first part, but I'll have a go:
Difficulty rating: 4/5.
Let the sequence
Now there exists some real number
Hence we can deduce that:
Now as
Hence there exists a sequence
This will occur in a situation where
