Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013-14 MX1 Marathon (archive) (1 Viewer)
- Thread starter SpiralFlex
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
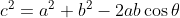
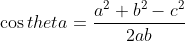
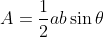
^2 )
^2} )
^2}{4a^2b^2}} )
^2} )
)(2ab+(a^2+b^2-c^2))} )
^2)((a+b)^2-c^2} )
)(c+a-b))(a+b-c)(a+b+c)} )
 \cdot 0.5(c+a-b) \cdot 0.5(a+b-c) \cdot 0.5(a+b+c)} )
(s-b)(s-c)} )
=========================================
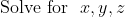
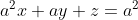
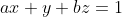
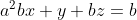
Let theta be an angle in the triangle.
=========================================
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
= ∫√x √sin^4 x - 2sin^2 x + 1 .dx
= ∫√x √(sin^2 x -1)^2
= ∫√x √(-cos^2 x)^2
= ∫√x |cos^2 x|.dx
There are no limits/borders, hence we ignore the absolute sign
∫√x cos^2 x.dx
Is this possible?
Let us factorise the x out and notice a perfect square
= ∫√x √sin^4 x - 2sin^2 x + 1 .dx
= ∫√x √(sin^2 x -1)^2
= ∫√x √(-cos^2 x)^2
= ∫√x |cos^2 x|.dx
There are no limits/borders, hence we ignore the absolute sign
∫√x cos^2 x.dx
Is this possible?
Last edited:
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
Ur equation has no negative sign, hence its not a SHM
In a simple harmonic motion(SHM), acceleration is defined as x(dot dot) = - n^2 x
Ur equation has no negative sign, hence its not a SHM
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
Lol don't worry about that question, I stuffed it up.Let us factorise the x out and notice a perfect square
= ∫√x √sin^4 x - 2sin^2 x + 1 .dx
= ∫√x √(sin^2 x -1)^2
= ∫√x √(-cos^2 x)^2
= ∫√x |cos^2 x|.dx
There are no limits/borders, hence we ignore the absolute sign
∫√x cos^2 x.dx
Is this possible?
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
Definately a 3U question:
 = x^5 - 5cx + 1, $ $ where c is a real number. \\ \\ $$(a) By considering the turning points, prove that if c $< 0, $ P(x) has just one real root, which is negative. \\ \\ $$(b) Prove that P(x) has three distinct real roots if and only if c $> \left ( \frac{1}{4} \right )^\frac{4}{5}.)
Definately a 3U question:
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Re: HSC 2013 3U Marathon Thread
Oh shet. I fixed that up afterward but ceebs to edit since no one did it. thanks for the note.In a simple harmonic motion(SHM), acceleration is defined as x(dot dot) = - n^2 x
Ur equation has no negative sign, hence its not a SHM
omgiloverice
Member
- Joined
- May 11, 2012
- Messages
- 160
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread

I'll do part b later when I have time to teach myself SHM
I'll do part b later when I have time to teach myself SHM
Attachments
-
39.4 KB Views: 361
Last edited:
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
Change cotθ into cosθ/sinθ, it'll make everything neater! ^^
Change cotθ into cosθ/sinθ, it'll make everything neater! ^^
shongaponga
Member
- Joined
- Feb 15, 2012
- Messages
- 125
- Gender
- Male
- HSC
- 2012
omgiloverice
Member
- Joined
- May 11, 2012
- Messages
- 160
- Gender
- Male
- HSC
- 2013
shongaponga
Member
- Joined
- Feb 15, 2012
- Messages
- 125
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 3U Marathon Thread
Note that the shortest distance between 2 points is a straight line.
Reflecting Island 1 as shown yields 2 triangles that are similar.
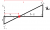
Therefore, using properties of similar triangles:
2/(6-x) = 1/x => 2x = 6-x => x = 2. And this must be the smallest value for x due to the above note. No calculus required!
Well done, was quiet a straight forward question i must admit and the only reason i posted it was because i was hoping someone would post a non-calculus solution. It can be done very elegantly as follows:
Note that the shortest distance between 2 points is a straight line.
Reflecting Island 1 as shown yields 2 triangles that are similar.

Therefore, using properties of similar triangles:
2/(6-x) = 1/x => 2x = 6-x => x = 2. And this must be the smallest value for x due to the above note. No calculus required!
Attachments
-
6.1 KB Views: 53
-
3.8 KB Views: 52
Last edited:
Makematics
Well-Known Member
Re: HSC 2013 3U Marathon Thread
(a) P'(x)=5x^4 -5c
To find any stationary points, solve P'(x)=0
5x^4 -5c=0
x^4 =c
x = ±∜c
But since c<0, ∜c is undefined and hence there are no stationary points.
P(0)=0-0+1
= 1
Also since c<0, we notice that P'(x)>0 for all real x, and hence P(x) is monotonic increasing.
By sketching a possible graph of P(x), we can clearly see that P(x) will have only one root, and that this root will be negative.
(b) The abscissae of the two stationary points are ∜c and -∜c.
P(∜c)=(∜c)^5 -5c(∜c) + 1
=c^(5/4) -5c^(5/4) + 1
= 1 - 4c^(5/4)
P(-∜c)=(-∜c)^5 -5c(-∜c) + 1
=-c^(5/4) +5c^(5/4) + 1
= 1 + 4c^(5/4)
By considering a graph of P(x), we can tell that there will be 3 distinct real roots if the product of the y coordinates is negative. i.e. one turning point is above the x-axis, one turning point is below the x-axis.
∴P(x) has three distinct real roots iff P(∜c).P(-∜c) < 0
P(∜c).P(-∜c)= [1 - 4c^(5/4)].[1 + 4c^(5/4)]
= 1 - 16c^(5/2)
= 1 - [4c^(5/4)]^2
< 0
1 - [4c^(5/4)]^2 < 0
[4c^(5/4)]^2 > 1
4c^(5/4) > 1
c^(5/4) > 1/4
c^5 > (1/4) ^4
c > (1/4) ^(4/5)
∴ P(x) has three distinct roots if and only if c > (1/4) ^(4/5).
fuuuu someone teach me how to use latex...
Definately a 3U question:
 = x^5 - 5cx + 1, $ $ where c is a real number. \\ \\ $$(a) By considering the turning points, prove that if c $< 0, $ P(x) has just one real root, which is negative. \\ \\ $$(b) Prove that P(x) has three distinct real roots if and only if c $> \left ( \frac{1}{4} \right )^\frac{4}{5}.)
(a) P'(x)=5x^4 -5c
To find any stationary points, solve P'(x)=0
5x^4 -5c=0
x^4 =c
x = ±∜c
But since c<0, ∜c is undefined and hence there are no stationary points.
P(0)=0-0+1
= 1
Also since c<0, we notice that P'(x)>0 for all real x, and hence P(x) is monotonic increasing.
By sketching a possible graph of P(x), we can clearly see that P(x) will have only one root, and that this root will be negative.
(b) The abscissae of the two stationary points are ∜c and -∜c.
P(∜c)=(∜c)^5 -5c(∜c) + 1
=c^(5/4) -5c^(5/4) + 1
= 1 - 4c^(5/4)
P(-∜c)=(-∜c)^5 -5c(-∜c) + 1
=-c^(5/4) +5c^(5/4) + 1
= 1 + 4c^(5/4)
By considering a graph of P(x), we can tell that there will be 3 distinct real roots if the product of the y coordinates is negative. i.e. one turning point is above the x-axis, one turning point is below the x-axis.
∴P(x) has three distinct real roots iff P(∜c).P(-∜c) < 0
P(∜c).P(-∜c)= [1 - 4c^(5/4)].[1 + 4c^(5/4)]
= 1 - 16c^(5/2)
= 1 - [4c^(5/4)]^2
< 0
1 - [4c^(5/4)]^2 < 0
[4c^(5/4)]^2 > 1
4c^(5/4) > 1
c^(5/4) > 1/4
c^5 > (1/4) ^4
c > (1/4) ^(4/5)
∴ P(x) has three distinct roots if and only if c > (1/4) ^(4/5).
fuuuu someone teach me how to use latex...
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread

Very nice! Excellently done, same method as mine(a) P'(x)=5x^4 -5c
To find any stationary points, solve P'(x)=0
5x^4 -5c=0
x^4 =c
x = ±∜c
But since c<0, ∜c is undefined and hence there are no stationary points.
P(0)=0-0+1
= 1
Also since c<0, we notice that P'(x)>0 for all real x, and hence P(x) is monotonic increasing.
By sketching a possible graph of P(x), we can clearly see that P(x) will have only one root, and that this root will be negative.
(b) The abscissae of the two stationary points are ∜c and -∜c.
P(∜c)=(∜c)^5 -5c(∜c) + 1
=c^(5/4) -5c^(5/4) + 1
= 1 - 4c^(5/4)
P(-∜c)=(-∜c)^5 -5c(-∜c) + 1
=-c^(5/4) +5c^(5/4) + 1
= 1 + 4c^(5/4)
By considering a graph of P(x), we can tell that there will be 3 distinct real roots if the product of the y coordinates is negative. i.e. one turning point is above the x-axis, one turning point is below the x-axis.
∴P(x) has three distinct real roots iff P(∜c).P(-∜c) < 0
P(∜c).P(-∜c)= [1 - 4c^(5/4)].[1 + 4c^(5/4)]
= 1 - 16c^(5/2)
= 1 - [4c^(5/4)]^2
< 0
1 - [4c^(5/4)]^2 < 0
[4c^(5/4)]^2 > 1
4c^(5/4) > 1
c^(5/4) > 1/4
c^5 > (1/4) ^4
c > (1/4) ^(4/5)
∴ P(x) has three distinct roots if and only if c > (1/4) ^(4/5).
fuuuu someone teach me how to use latex...
Attachments
-
16.9 KB Views: 288
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 3U Marathon Thread
=3)
=3)
Split the integral into:
~dx + \int_{0.5}^{1.5} I(x)~dx + \int_{1.5}^{2.5} I(x)~dx + ... + \int_{n-1.5}^{n-0.5} I(x)~dx + \int_{n-0.5}^{n})
Now in each of these intervals,) is 0, 1, 2, ..., n respectively for each term. I.e. the first term is integral
is 0, 1, 2, ..., n respectively for each term. I.e. the first term is integral =0) , the second integral
, the second integral =1) up to the last integral where
up to the last integral where =n)
Hence we arrive at:
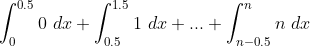
Which upon evaluation becomes:
+\frac{n}{2})
Note the last term is divided by 2 as the interval we are integrating over is halved. Summing this gives:
}{2} + \frac{n}{2})
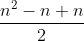
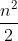
#
Split the integral into:
Now in each of these intervals,
Hence we arrive at:
Which upon evaluation becomes:
Note the last term is divided by 2 as the interval we are integrating over is halved. Summing this gives:
#
- Status
- Not open for further replies.