-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (4 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
continuing from where i was...
^2} = \frac{1}{2} \int_{0}^{\pi/2} \frac{dx}{(\sqrt{2}sin(x + \pi/4))^2} \\ = \frac{1}{4} \int_{0}^{\pi/2}\frac{dx}{sin^2 (x+\pi/4)} \\ = \frac{1}{4} \int_{0}^{\pi/2} cosec^2 (x+\pi/4)dx \\ =\frac{1}{4}\left [ -cot(x+ \pi/4) \right ]_0 ^{\pi/2} \\ = -\frac{1}{4}\left [ cot(\frac{3\pi}{4}) - cot(\frac{\pi}{4}) \right ] \\ = -\frac{1}{4} \left ( -1 - 1 \right ) \\ = \frac{1}{2})
That is an odd question..... wth..
sorry i made a mistake...
continuing from where i was...
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
YEp something like that, nice work.That is an odd question..... wth..
use the property that
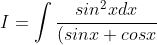^2} \\ $Use the property \\ \therefore I= $\int \frac{cos^2 x dx}{(cosx + sinx)^2} \\ \\ 2I = \int \frac{dx}{(sinx + cosx)^2} \\ I = \frac{1}{2} \int \frac{dx}{1 + 2sinxcosx} \\ \therefore I = \frac{1}{2} . \frac{sinx}{cosx + sinx} + C ($by using t = tan(x/2), but too lazy to post it up...))
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
i c wut u did tharThat is an odd question..... wth..
Re: HSC 2013 4U Marathon
} dx = \int \frac {dtanx}{sec^2 x + 2tan x} \\ \\ = \int \frac {dtan x}{tan^2 x + 2tan x + 1} = \int \frac {1}{(1+tanx)^2}d(1+tanx) = - \frac {1}{1+tanx} + C )
 if you prefer.
if you prefer.
I tried out the t-method as suggested but did not end up with a nice expression. Maybe I made a mistake along the way. But we can integrate without the t-method this way:YEp something like that, nice work.
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Let a < b be two consecutive roots of a polynomial P(x), (so P is nonzero between a and b). Suppose these roots are each of multiplicity 1, so that:
P(x)=(x-a)(x-b)g(x)
for some polynomial g(x) with g(a),g(b) != 0 by the factor theorem.
1. Prove that g(a) and g(b) have the same sign.
2. Prove there is a real number c between a and b with f'(c)=0.
3. Prove that (2) is true even if we drop the assumption that the roots a and b are of multiplicity 1.
4. Draw a picture and give a geometric description of this result.
(This is a special case of the Mean Value theorem, one of the most important theorems in differential calculus. The general proof of the MVT is beyond the scope of MX2, but we know enough about polynomials to be able to prove this special case.)
Let a < b be two consecutive roots of a polynomial P(x), (so P is nonzero between a and b). Suppose these roots are each of multiplicity 1, so that:
P(x)=(x-a)(x-b)g(x)
for some polynomial g(x) with g(a),g(b) != 0 by the factor theorem.
1. Prove that g(a) and g(b) have the same sign.
2. Prove there is a real number c between a and b with f'(c)=0.
3. Prove that (2) is true even if we drop the assumption that the roots a and b are of multiplicity 1.
4. Draw a picture and give a geometric description of this result.
(This is a special case of the Mean Value theorem, one of the most important theorems in differential calculus. The general proof of the MVT is beyond the scope of MX2, but we know enough about polynomials to be able to prove this special case.)
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
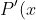 = (2x-(a+b))g(x) + g'(x) (x-a)(x-b) )
If a and b are consecutive roots, then it is easy to see that P'(a) and P'(b) are opposite in sign by drawing a picture. They can't be zero since they have roots of multiplicity of 1.
 = (a-b) g(a) )
 = (b-a) g(b) )
Since a < b, let us denote a sign (positive or negative) as (1) and the other as (2)
So IF P'(a) has sign (1), and since P'(a) = (a-b) g(a), since a < b then g(a) has sign (2)
Since P'(b) is opposite in sign, it will have sign (2)
IF P'(b) has sign (2), since b-a > 0, then g(b) has sign (2)
Therefore g(a) and g(b) have the same sign.
2.
(I assume you mean P'(c) = 0 )
Since P'(a) and P'(b) have OPPOSITE gradient, therefore there must exist a point (since P is a polynomial and is therefore continuous) that P'(c) is zero.
3.
IF the multiplicity of a and/or b are greater than 1, then the P'(a) and/or P'(b) are zero. But that doesn't matter since for some value, P'(a+) (some value to the right of a), will either be positive or negative, therefore the polynomial is either increasing or decreasing.
No matter what the orientation, the curve must curve back to zero as b is a root as well. Since it must curve back there must exist some point where the curve has zero gradient. (easier explained by a picture).
4.
*coming soon*
======
1.Let a < b be two consecutive roots of a polynomial P(x), (so P is nonzero between a and b). Suppose these roots are each of multiplicity 1, so that:
P(x)=(x-a)(x-b)g(x)
for some polynomial g(x) with g(a),g(b) != 0 by the factor theorem.
1. Prove that g(a) and g(b) have the same sign.
2. Prove there is a real number c between a and b with f'(c)=0.
3. Prove that (2) is true even if we drop the assumption that the roots a and b are of multiplicity 1.
4. Draw a picture and give a geometric description of this result.
(This is a special case of the Mean Value theorem, one of the most important theorems in differential calculus. The general proof of the MVT is beyond the scope of MX2, but we know enough about polynomials to be able to prove this special case.)
If a and b are consecutive roots, then it is easy to see that P'(a) and P'(b) are opposite in sign by drawing a picture. They can't be zero since they have roots of multiplicity of 1.
Since a < b, let us denote a sign (positive or negative) as (1) and the other as (2)
So IF P'(a) has sign (1), and since P'(a) = (a-b) g(a), since a < b then g(a) has sign (2)
Since P'(b) is opposite in sign, it will have sign (2)
IF P'(b) has sign (2), since b-a > 0, then g(b) has sign (2)
Therefore g(a) and g(b) have the same sign.
2.
(I assume you mean P'(c) = 0 )
Since P'(a) and P'(b) have OPPOSITE gradient, therefore there must exist a point (since P is a polynomial and is therefore continuous) that P'(c) is zero.
3.
IF the multiplicity of a and/or b are greater than 1, then the P'(a) and/or P'(b) are zero. But that doesn't matter since for some value, P'(a+) (some value to the right of a), will either be positive or negative, therefore the polynomial is either increasing or decreasing.
No matter what the orientation, the curve must curve back to zero as b is a root as well. Since it must curve back there must exist some point where the curve has zero gradient. (easier explained by a picture).
4.
*coming soon*
======
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Good, although your answer to 3. is more of a plausibility argument than a proof. The point is to do it in a similar way to to 2, using that a continuous function can only change sign on an interval if it possesses a root on this interval.1.
If a and b are consecutive roots, then it is easy to see that P'(a) and P'(b) are opposite in sign by drawing a picture. They can't be zero since they have roots of multiplicity of 1.
Since a < b, let us denote a sign (positive or negative) as (1) and the other as (2)
So IF P'(a) has sign (1), and since P'(a) = (a-b) g(a), since a < b then g(a) has sign (2)
Since P'(b) is opposite in sign, it will have sign (2)
IF P'(b) has sign (2), since b-a > 0, then g(b) has sign (2)
Therefore g(a) and g(b) have the same sign.
2.
(I assume you mean P'(c) = 0 )
Since P'(a) and P'(b) have OPPOSITE gradient, therefore there must exist a point (since P is a polynomial and is therefore continuous) that P'(c) is zero.
3.
IF the multiplicity of a and/or b are greater than 1, then the P'(a) and/or P'(b) are zero. But that doesn't matter since for some value, P'(a+) (some value to the right of a), will either be positive or negative, therefore the polynomial is either increasing or decreasing.
No matter what the orientation, the curve must curve back to zero as b is a root as well. Since it must curve back there must exist some point where the curve has zero gradient. (easier explained by a picture).
4.
*coming soon*
======
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon

wow! very nice! thank u for sharingI tried out the t-method as suggested but did not end up with a nice expression. Maybe I made a mistake along the way. But we can integrate without the t-method this way:
if you prefer.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
(You must also assume that q is not the square of a rational number.)
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Am interested in seeing peoples solutions actually. This is a v.good question because it is not very technically demanding at all, but if you don't properly understand the relevant part of the MX2 course you probably won't have any chance of solving it. ie it slay rote learners.
Am interested in seeing peoples solutions actually. This is a v.good question because it is not very technically demanding at all, but if you don't properly understand the relevant part of the MX2 course you probably won't have any chance of solving it. ie it slay rote learners.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon

Ah yeah oops(You must also assume that q is not the square of a rational number.)
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
You'd also have to note the polynomial is not monic. Though I guess this is a consequence of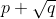 being a root.
being a root.
You'd also have to note the polynomial is not monic. Though I guess this is a consequence of
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Huh? The result is still true for monic polynomials...and having a root of the form p+q^{1/2} is perfectly possible for monic polynomials.You'd also have to note the polynomial is not monic. Though I guess this is a consequence ofbeing a root.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
Nevermind I derped and thought the root was rational after reading "p and q are rational" without considering the square root.Huh? The result is still true for monic polynomials...and having a root of the form p+q^{1/2} is perfectly possible for monic polynomials.
- Status
- Not open for further replies.

