Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Volumes ?? (1 Viewer)
- Thread starter Currybear
- Start date
Makematics
Well-Known Member
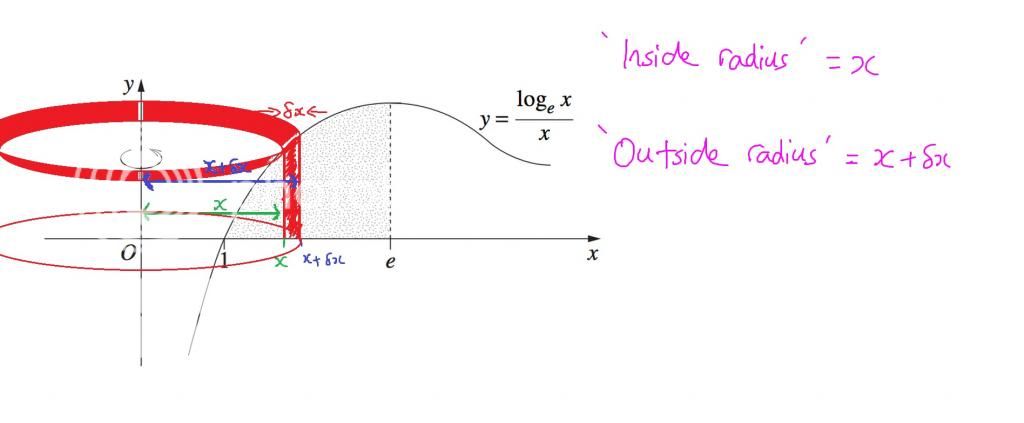
so you draw in a strip of delta x and you can assign an arbitrary point (x,y) on the curve at the top left hand corner of the (almost) rectangular strip. from there, it should be clear that the inner radius of the shell will be x, and the outer radius will be x+deltax.
Yes of course. A typical slice of area is drawn parallel to the axis of rotation (the y-axis). The distance from the y-axis to this slice is x, and after rotating this slice it becomes the radius of the shell.so the radius isn't measured from the axis of rotation?
Remember: For slicing, draw your typical slice perpendicular to the axis of rotation; for shells draw it parallel to the axis of rotation.
Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Hopefully this clears something up. We are working with a 3D object, so there is no single 'radius' for an open cylinder (since it has some thickness delta x). There are two radii being X and X+deltaX.so the radius isn't measured from the axis of rotation?
If you are using the 'unfold the shell to form a thin rectangular prism' method, then you will need a single 'radius. However, you may assume this radius to be X instead of delta X because we are eventually allowing delta X to approach zero, so for ease of computations (without any error in calculation), we may assume that the 'radius' is simply X.
But if you are doing it the 'Find area of annulus, multiply by height' method ie: pi*(R^2-r^2)h, then your R would be x+deltax and r would be x, where R > r.
Last edited:
Hi Carrotsticks,Hopefully this clears something up. We are working with a 3D object, so there is no single 'radius' for an open cylinder (since it has some thickness delta x). There are two radii being X and X+deltaX.
If you are using the 'unfold the shell to form a thin rectangular prism' method, then you will need a single 'radius. However, you may assume this radius to be X instead of delta X because we are eventually allowing delta X to approach zero, so for ease of computations (without any error in calculation), we may assume that the 'radius' is simply X.
But if you are doing it the 'Find area of annulus, multiply by height' method ie: pi*(R^2-r^2)h, then your R would be x+deltax and r would be x, where R > r.

I could be wrong, but based on his question I think Currybear's problem was not knowing the orientation of the slice - ie. parallel to the y-axis.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
I am not 100% sure, but I'll leave it until Currybear responds.Hi Carrotsticks,
I could be wrong, but based on his question I think Currybear's problem was not knowing the orientation of the slice - ie. parallel to the y-axis.
Makematics
Well-Known Member
i think it is true, but i wouldn't recommend rote learning volumes. there isn't always one method that will suit all the cylindrical shells questions. you have to be able to adapt your thinking to deal with harder questions involving. for example my teacher gave us a question in which y=x was the axis of rotation.so for all cyndrical shells rotated about the y axis or an x= something, the radius is always x?
If you rotate about the line x=a, then the radius is |x-a|.so for all cyndrical shells rotated about the y axis or an x= something, the radius is always x?
and rotating around the line y=a, gives radius y-a?If you rotate about the line x=a, then the radius is |x-a|.
The radius is actually |y-a|, but as you will be squaring the radius you can omit the absolute value.and rotating around the line y=a, gives radius y-a?
However if you use the method of unrolling the shell to form a rectangular prism of area 2.pi.r.h, the radius is not squared, so you have to be careful about the direction of the subtraction when finding r.


