Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Mathematical Curiosities. (1 Viewer)
- Thread starter Carrotsticks
- Start date
- Joined
- Feb 16, 2005
- Messages
- 8,578
- Gender
- Male
- HSC
- 2006
Not sure if this belongs here, but I've always wondered whether it is possible to prove
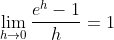
using methods within the constraints of the HSC syllabus (especially 2 unit).
Reason I asked is because this is a necessary component to prove that
=e^x)
from first principles and all the 'proofs' I've seen so far within the HSC syllabus are just numerical substitutions for small values of h.
using methods within the constraints of the HSC syllabus (especially 2 unit).
Reason I asked is because this is a necessary component to prove that
from first principles and all the 'proofs' I've seen so far within the HSC syllabus are just numerical substitutions for small values of h.
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Yeah some juggling results in usingActually nvm, just realised it was related to the definition of e as a limit.
omgiloverice
Member
- Joined
- May 11, 2012
- Messages
- 160
- Gender
- Male
- HSC
- 2013
Here is few questions I have being attempting to solve lately.
How can I derive the length of an curve between two values of x? (I tried using Pythagoras for dx, dy, and dl, where dl is an infinity small length on an curve, however I don't think this approach is right)
I still have my unsolved question here: http://community.boredofstudies.org/showthread.php?t=296191&p=6440822#post6440822
i have more but I want to sleep
What is the square root of negative 'i'?
What is the reason for the t formula?
Can you prove Pythagoras theorem by calculus?
Is it possible to find the volume and surface area of any abstract 3D object. (like the opera house)
why is the directrix so important other then deriving the formula for a parabola?
Are there inequalities in a 2 dimensional form?
Now I am going to go more into mathematical physics if that doesn't bother anyone
Is it possible to form an parametric equation for a double pendulum system, if the end of the pendulum starts at the origin?
How do you derive Newtons Law of Universal Gravitation from first principles, and how would the gravity work if you were on an ellipsoid or any other odd shape? (like a square)
How can I derive the length of an curve between two values of x? (I tried using Pythagoras for dx, dy, and dl, where dl is an infinity small length on an curve, however I don't think this approach is right)
I still have my unsolved question here: http://community.boredofstudies.org/showthread.php?t=296191&p=6440822#post6440822
i have more but I want to sleep
What is the square root of negative 'i'?
What is the reason for the t formula?
Can you prove Pythagoras theorem by calculus?
Is it possible to find the volume and surface area of any abstract 3D object. (like the opera house)
why is the directrix so important other then deriving the formula for a parabola?
Are there inequalities in a 2 dimensional form?
Now I am going to go more into mathematical physics if that doesn't bother anyone
Is it possible to form an parametric equation for a double pendulum system, if the end of the pendulum starts at the origin?
How do you derive Newtons Law of Universal Gravitation from first principles, and how would the gravity work if you were on an ellipsoid or any other odd shape? (like a square)
Last edited:
anomalousdecay
Premium Member
- Joined
- Jan 26, 2013
- Messages
- 5,757
- Gender
- Male
- HSC
- 2013
When I was doing my 2-unit half-yearly, a question asked to use the SI table to do a question, which I did normally.
I finished the test in half the time allocated, got really bored, and decided to play around with the case a little.
Now I will do the normal integration question from the case given:
 + C_1 )
Now I integrated this question in a different manner, using complex identity:
 + C_2 )
Would it be safe from here to assume that:
 + C_2 = log_{e}(x+\sqrt{x^2-a^2}) + C_1 )
What if you use some sort of limits in this question? will it help to show some kind of valid proof?
For example:

From above:
 = log_{e}(x+\sqrt{x^2-a^2}) )
 } = x+\sqrt{x^2-a^2} )
Is it possible to solve for x here? Is any part of my working wrong and against mathematical rules?
I finished the test in half the time allocated, got really bored, and decided to play around with the case a little.
Now I will do the normal integration question from the case given:
Now I integrated this question in a different manner, using complex identity:
Would it be safe from here to assume that:
What if you use some sort of limits in this question? will it help to show some kind of valid proof?
For example:
From above:
Is it possible to solve for x here? Is any part of my working wrong and against mathematical rules?
Last edited:
RealiseNothing
what is that?It is Cowpea
anomalousdecay
Premium Member
- Joined
- Jan 26, 2013
- Messages
- 5,757
- Gender
- Male
- HSC
- 2013
You were too quick. I was fixing up my latex codes.What?
anomalousdecay
Premium Member
- Joined
- Jan 26, 2013
- Messages
- 5,757
- Gender
- Male
- HSC
- 2013
Your factorisation was incorrect. It only works for reals!
We can see the fallacy if we extend it a little:
It comes from the famous proof that i^2 = 1:
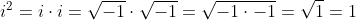
Ahh thanks. Now I get it. I posted something similar on that fallacy ages ago in this thread. Its amazing how we use that method all the time or real numbers, yet it does not apply to complex numbers.
I'm wondering though if there is a way to factorise it properly and get some other types of integrals.
Year 12. That was my last 2-unit exam and I was fully prepared to do 4-unit.What year were you in when you did this exam anomalous?
I never actually finished the 2-unit course lol. I never did the financial stuff and skipped a lot of 2-unit probability (that is probably the reason why I tend to have problems drawing tree diagram and understand what I am doing).
4025808
Well-Known Member
I for one never knew why the BoS would not introduce some more statistics and some linear algebra into the syllabus. By all means we're going to use more of that stuff at uni so why not?
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
I think linear algebra would be completely unmotivated, as is first year LA. The most they would do is computational techniques like dot and cross products and matrices but their use and beauty, especially in proof would be too difficult for the average 4u student. Statistics would be similar - I know in the IB they do some first year stats but from what I've heard it's also largely unmotivated.I for one never knew why the BoS would not introduce some more statistics and some linear algebra into the syllabus. By all means we're going to use more of that stuff at uni so why not?
The current form has a more natural progression from 2 and 3 u, like polynomials, graphing, integration with some extra topics like mechanics (which is mostly computation anyway...) And introduces some stuff like inequalities and some harder induction proofs. Complex numbers is kind of dealt with in a superficial way but this is unavoidable given that complex analysis and calculus would be too difficult.
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Here is few questions I have being attempting to solve lately.
How can I derive the length of an curve between two values of x? (I tried using Pythagoras for dx, dy, and dl, where dl is an infinity small length on an curve, however I don't think this approach is right)
I still have my unsolved question here: HSC 2013 3U Marathon Thread - Page 22
i have more but I want to sleep
What is the square root of negative 'i'?
What is the reason for the t formula?
Can you prove Pythagoras theorem by calculus?
Is it possible to find the volume and surface area of any abstract 3D object. (like the opera house)
why is the directrix so important other then deriving the formula for a parabola?
Are there inequalities in a 2 dimensional form?
Now I am going to go more into mathematical physics if that doesn't bother anyone
Is it possible to form an parametric equation for a double pendulum system, if the end of the pendulum starts at the origin?
How do you derive Newtons Law of Universal Gravitation from first principles, and how would the gravity work if you were on an ellipsoid or any other odd shape? (like a square)
The t-formula transforms some trigonomic expressions into completely algebraic expressions that are usually easier to integrate. It has other applications obviously.
http://www.cut-the-knot.org/pythagoras/CalculusProof.shtml
Yes, as long as you have an equation that models it (be it piece wise or what) you can use some elementary calculus (in 3 dimenions) to figure these quantities out.
In terms of what? It is a fundamental object in the construction of all the conics (well, maybe not the circle) and so its properties are interesting.
Yes, imagine a surface in 3-D, that looks like this for example: http://www3.wolframalpha.com/Calcul...=240.&h=191.&cdf=MeshControl&cdf=RangeControl - the value of z is always equal to or above 1.
Yes but its just more complicated...
Use forces! Draw a free body diagram and try deriving it yourself
Last edited:
anomalousdecay
Premium Member
- Joined
- Jan 26, 2013
- Messages
- 5,757
- Gender
- Male
- HSC
- 2013
The opera house is already in the form of a few curves.Is it possible to find the volume and surface area of any abstract 3D object. (like the opera house)
why is the directrix so important other then deriving the formula for a parabola?
And how would the gravity work if you were on an ellipsoid or any other odd shape? (like a square)
And directrices are very important for glasses and telecommunication devices.
There is a point where concave and convex lenses diminish the picture (take a magnifying glass and you'll realise a point where the image is diminished.
That's Physics. But to imagine this concept you must understand the definition of Einstein's definition of gravity, not Newtonian gravity.
Basically its like imagining that space is a 3d fabric which warps on the basis of different densities. It is very hard to imagine it, but this is the 2d representation:

So now imagine what it would be like for a different shape, using this model. I will post up an extracurricular Physics thread on this. If you want to ask more, then post in there instead of here, which is for Maths.

