Re: HSC 2014 4U Marathon - Advanced Level
Here's a follow up question.
A clock has an hour-hand of 3 units and a minute-hand of 4 units. If the hands are currently positioned at three-o'-clock, determine the first time when the tips of the hands are moving away from each other the fastest
This is a bit tedious, so I won't include every detail, but I think this is right.
We can write the two hands endpoints in polar coordinates as
=(3,\pi/2+2\pi t) \quad (r_2,\theta_2)=(4,120\pi t).)
As the hands have constant angular speeds, and hand 2 is moving faster, the first time the tips are moving away the fastest will occur when
.)
We write
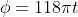
for brevity. (This is the angle between hands, offset by a constant factor of
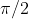
.)
If x is the separating distance, we have (using the cosine rule),
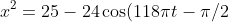=25-24\sin(\phi).)
Differentiating twice using the chain rule we get
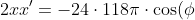)
and
^2+2xx''=24\cdot(118\pi)^2\cdot \sin(\phi).)
Now, at the time of interest, x'' vanishes, so plugging the expression for the first derivative of x into the second equation and simplifying we get
=25\sin(\phi)-24\sin^2(\phi).)
Use the Pythagorean identity to put everything in terms of sin(x), and factorise the resulting quadratic to get.
-4)(4\sin(\phi)-3)=0\Rightarrow \sin(\phi)=3/4.)
Since
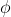
must lie in one of the second two quadrants (*), this gives
}{118\pi}.)
(Here t is the number of hours elapsed since the starting time of 3:00.)


