shongaponga
Member
- Joined
- Feb 15, 2012
- Messages
- 125
- Gender
- Male
- HSC
- 2012
Hey guys, I am attempting to prove a question that I found from a problem set from Stanford Uni on series and sequences, however I'm having a little bit of difficulty. I've been at it for a while and so finally i've resorted to looking at the provided solution. The question and solution are provided below:
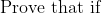
Provided Solution:
a_n \leq a_{N+1} + ... + a_n = |S_n - S_N| < \epsilon. $ Hence, $ \lim_{n\rightarrow \infty} (n-N)a_n=0. $ Thus we have$ \lim_{n\rightarrow \infty} N{a_n}=N\lim_{n\rightarrow \infty}{a_n}=0 $ too$, $ and this implies$ \lim_{n\rightarrow \infty} n{a_n} = \lim_{n\rightarrow \infty} (n-N)a_n + \lim_{n\rightarrow \infty}Na_n=0. ~~~~~~~~~~~$QED $ )
Now i recognized that S_n was Cauchy and hence for however this is as far as i was able to get (i had a bit more working but none of it got me much further towards a solution).
however this is as far as i was able to get (i had a bit more working but none of it got me much further towards a solution).
My questions are: (1) how isa_n \leq a_{N+1} + ... + a_n ?) ie i simply can't wrap my head around how this inequality holds (i understand it must have something to do with the fact that a_n is decreasing) - if someone could explain this that would be great! And (2) how would one be able to recognize that (n-N)a_n <= |S_n - S_N| < epsilon would lead to the final result? (eg clues/hints from the question?) It just doesn't come to me intuitively.
ie i simply can't wrap my head around how this inequality holds (i understand it must have something to do with the fact that a_n is decreasing) - if someone could explain this that would be great! And (2) how would one be able to recognize that (n-N)a_n <= |S_n - S_N| < epsilon would lead to the final result? (eg clues/hints from the question?) It just doesn't come to me intuitively.
Any help, (and alternative solutions) are much appreciated
Provided Solution:
Now i recognized that S_n was Cauchy and hence for
My questions are: (1) how is
Any help, (and alternative solutions) are much appreciated
Last edited:
