-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Marathon ADVANCED (archive) (3 Viewers)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
dan964
what
Re: HSC 2015 4U Marathon - Advanced Level
Note sure if correct:
<removed> fixed version 2 posts below
added RTP line.
Note sure if correct:
<removed> fixed version 2 posts below
added RTP line.
Last edited:
Re: HSC 2015 4U Marathon - Advanced Level
Your LHS in the 'RTP' line is not always less than 2.5. E.g. in an equilateral triangle, all angles are 60º, and cos(60º) = ½, so your LHS is then 2•(½ + ½ + ½) = 3.
dan964
what
Re: HSC 2015 4U Marathon - Advanced Level
It has been found.It was a dumb error in failing to carry a constant of 2 through on some terms.
<removed>
fixed version is below
I realised that and was trying to look for which line was wrong.Your LHS in the 'RTP' line is not always less than 2.5. E.g. in an equilateral triangle, all angles are 60º, and cos(60º) = ½, so your LHS is then 2•(½ + ½ + ½) = 3.
It has been found.It was a dumb error in failing to carry a constant of 2 through on some terms.
<removed>
fixed version is below
Last edited:
Re: HSC 2015 4U Marathon - Advanced Level
It still says LHS ≤ 2.5 on the second last line (this could just be a typo, I haven't read through the proof, just skimmed it).I realised that and was trying to look for which line was wrong.
It has been found.It was a dumb error in failing to carry a constant of 2 through on some terms.
View attachment 32240
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon - Advanced Level
nvmI realised that and was trying to look for which line was wrong.
It has been found.It was a dumb error in failing to carry a constant of 2 through on some terms.
View attachment 32240
Last edited:
dan964
what
Re: HSC 2015 4U Marathon - Advanced Level
Knowing the angles of a triangle isn't enough to determine a unique area, since the triangles could have different sizes for given angles (they would all be similar triangles).Can I post a question:
Needs fixing just wait...
You may assume or derive a suitable formula for the area of a triangle in terms of the sides or angles.
dan964
what
Re: HSC 2015 4U Marathon - Advanced Level

I'll rewrite it in latex for you:Show that 4m^2+17n^2 and 4n^2+17m^2 cannot be both be perfect squares, where n, and m are positive integers
simpleetal
Member
- Joined
- Apr 6, 2015
- Messages
- 54
- Gender
- Male
- HSC
- 2016
Re: HSC 2015 4U Marathon - Advanced Level
by letting each of the expressions equal to u^2 and v^2 respectively, we can deduce that m and n must both be odd for u and v to be integers. Hence, we only consider the case where m and n areboth odd integers. But this is a contradiction as for each expression, upon division by 8, we get a remainder of 5 on the lhs(all odd squares have remainder 1 when divided by 8) while on the rhs we have remainder 1 (since u and v are both odd if m, n both odd)Show that 4m^2+17n^2 and 4n^2+17m^2 cannot be both be perfect squares, where n, and m are positive integers
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
Finishing off the cubic question (finally!):
It remains to show that for a polynomial with three real roots, the inequalities:
1. |bd-c| < 1-d^2
and
2. |b+d| < |1+c|
imply that all three roots live in the open unit interval.
As discussed in my previous posts, inequality 2 implies that p(1) > 0 and p(-1) < 0, which means there is at least one real root in the unit interval.
If all three roots DON'T live in the unit interval then either two of them are at least 1 or two of them are at most -1. (By considering the limiting behaviour of p at +inf and -inf.)
Let us assume we are in one of these cases for the sake of contradiction.
For inequality 1 to hold, we must of course have d^2 < 1. (*)
We also have that the polynomial q(1)= 1-d^2 - (c-bd) >= 1-d^2 - |c-bd| > 0. (q was defined earlier as the polynomial with roots the pairwise products of the roots of p).
This means that either zero or two of the quantities
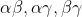
exceed 1, with the others being less than 1. (**)
As at least two of these roots have the same sign, this observation implies that all three roots must have the same sign.
So we are left with the possibilities:
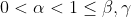
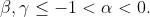
In the first of these, we have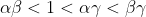 from (**).
from (**).
This means we can multiply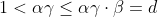
which contradicts (**).
Similarly, in the latter of the two possibilities, we have:
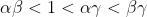
So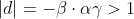
again in contradiction with (**).
This completes the proof.
Finishing off the cubic question (finally!):
It remains to show that for a polynomial with three real roots, the inequalities:
1. |bd-c| < 1-d^2
and
2. |b+d| < |1+c|
imply that all three roots live in the open unit interval.
As discussed in my previous posts, inequality 2 implies that p(1) > 0 and p(-1) < 0, which means there is at least one real root in the unit interval.
If all three roots DON'T live in the unit interval then either two of them are at least 1 or two of them are at most -1. (By considering the limiting behaviour of p at +inf and -inf.)
Let us assume we are in one of these cases for the sake of contradiction.
For inequality 1 to hold, we must of course have d^2 < 1. (*)
We also have that the polynomial q(1)= 1-d^2 - (c-bd) >= 1-d^2 - |c-bd| > 0. (q was defined earlier as the polynomial with roots the pairwise products of the roots of p).
This means that either zero or two of the quantities
exceed 1, with the others being less than 1. (**)
As at least two of these roots have the same sign, this observation implies that all three roots must have the same sign.
So we are left with the possibilities:
In the first of these, we have
This means we can multiply
which contradicts (**).
Similarly, in the latter of the two possibilities, we have:
So
again in contradiction with (**).
This completes the proof.
Last edited:
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: HSC 2015 4U Marathon - Advanced Level
Find all functions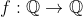 such that
such that
=f(x)f(y)-f(x+y)+1)
for all rational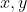 .
.
(Note that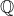 is the set of rational numbers.)
is the set of rational numbers.)
Find all functions
for all rational
(Note that
VBN2470
Well-Known Member
Re: HSC 2015 4U Marathon - Advanced Level
 to get
to get =f(0)^2-f(0)+1 \Rightarrow (f(0)-1)^2=0 \Rightarrow f(0)=1 ) . Not sure how to go from there..
. Not sure how to go from there.. 
I can see that the function defined by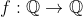 such that
such that =1 ) is a solution, but not sure how to show it (let alone other possible solutions).
is a solution, but not sure how to show it (let alone other possible solutions).
SetFind all functionssuch that
for all rational.
(Note thatis the set of rational numbers.)
I can see that the function defined by
VBN2470
Well-Known Member
Re: HSC 2015 4U Marathon - Advanced Level
 , but got an equation which I'm not sure how to manipulate..
, but got an equation which I'm not sure how to manipulate..
Not too experienced/familiar with these functional equations.
I tried that as well as plugging in
Not too experienced/familiar with these functional equations.
VBN2470
Well-Known Member
Re: HSC 2015 4U Marathon - Advanced Level
 , I think you meant
, I think you meant  but instead you wrote
but instead you wrote  which should instead give
which should instead give =f(x)^2-f(2x)+1 ) .. (3 posts ago)
.. (3 posts ago)
Yep I got that for
simpleetal
Member
- Joined
- Apr 6, 2015
- Messages
- 54
- Gender
- Male
- HSC
- 2016
Re: HSC 2015 4U Marathon - Advanced Level
I'll do this in two separate posts, because otherwise the equation is too long
=f(x)f(y)-f(x+y)+1.$ It's already been established that $f(0)=1, $and letting x=-1, and y=1 (to somehow try make use of f(0)), we get that$ f(-1)=f(-1)f(1),$ so we consider two cases:f(-1)=0 or f(1)=1. $f(1)=1,$ then, by letting y=1, we get $f(x)=f(1)-f(x+1)+1,$ and thus$ f(x+1)=1, $or$ f(x)=1.\\$ If$ f(-1)=0, $then by letting y=-1, (to try get an expression involving f(-1)) we get that $f(-x)=f(x)f(-1)-f(x-1)+1. $Thus,$ f(-x)=1-f(x-1).$Call this equation A. Subbing this into original equation, we get that $f(-xy)=(1-f(x-1))f(y)-f(-x+y)+1\rightarrow 1-f(xy-1)=(1-f(x-1))f(y)-f(-x+y)+1.$ The ones cancel off, so we get$ (1-f(x-1))f(y)-f(-x+y)+f(xy-1)=0.$ Letting x=2, and y=1, we get that$ f(1)-f(1)^2-f(-1)+f(1),$ and f(-1)=0, so (2-f(1))(f(1))=0. \\So f(1)=$2 or 0$. )
I'll do this in two separate posts, because otherwise the equation is too long
Last edited:
- Status
- Not open for further replies.

