-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Factorisation (1 Viewer)
- Thread starter Blitz_N7
- Start date
I am going to guess that your first line is an intermediate stage in your working for a different question.Is there a way to factorise:
m^3 -3m^2 +2m +3m^2n-3mn+3mn^2-3mn+n^3-3n^2+2n into:
(m-n)(m-n-1)(m-n-2)? Thx in advance.
If so, could you post the actual question - there might be an easier way to do it.
Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,615
- Gender
- Male
- HSC
- 2015
I got (m+n)(m+n-1)(m+n-2), is there something wrong with the question or am I simply wrong?Is there a way to factorise:
m^3 -3m^2 +2m +3m^2n-3mn+3mn^2-3mn+n^3-3n^2+2n into:
(m-n)(m-n-1)(m-n-2)? Thx in advance.
Edit: After doing some expansion, I realised that multiplying -n three times will not give positive n^3, so there must be something wrong with the answer
Last edited:
Much more easily done combinatorially than algebraically.The actual question is proving: (m+n)C3=mC3+mC2nC1+mC1nC2+nC3. Combinations :/
rand_althor
Active Member
- Joined
- May 16, 2015
- Messages
- 554
- Gender
- Male
- HSC
- 2015
It is easier if you consider the coefficient of 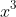 in
in 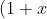^{m+n}) and
and 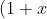^m(1+x)^n) . You know that the coefficients of
. You know that the coefficients of 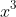 in each of these expansions will be equal as
in each of these expansions will be equal as 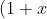^m(1+x)^n=(1+x)^{m+n}) .
.
Last edited:
Blitz_N7
Member
- Joined
- May 27, 2015
- Messages
- 51
- Gender
- Undisclosed
- HSC
- 2016
Thank you!
Blitz_N7
Member
- Joined
- May 27, 2015
- Messages
- 51
- Gender
- Undisclosed
- HSC
- 2016
Thank you!If you still want to know how to do it algebraically:
((m+n)^2 -3(m+n) + 2 )= (m+n)(m+n-1)(m+n-2) )
YouCantMakeMe
Member
- Joined
- Oct 5, 2015
- Messages
- 46
- Gender
- Undisclosed
- HSC
- N/A
How would you articulate this in an exam? Nice math skills
Probably just write it similarly to that (though you probably wouldn't need full sentences), and maybe draw a diagram if it helps, like:How would you articulate this in an exam? Nice math skills
where each * represents a distinct object.
YouCantMakeMe
Member
- Joined
- Oct 5, 2015
- Messages
- 46
- Gender
- Undisclosed
- HSC
- N/A
And nice LaTex skills haha.Probably just write it similarly to that (though you probably wouldn't need full sentences), and maybe draw a diagram if it helps, like:
where each * represents a distinct object.
