Was the Brouwer fixed point theorem used by Nash to prove the existence of a Nash Equilibrium in a game or something? I don't know too much about game theory haha but this was something I think I heard. And is your use of Russia as the country at all a subtle reference to this game theory of Nash's time? Lol (seems too coincidental that you chose RussiaI have always found fixed point theorems quite pretty.
Probably the most well-known one is the Brouwer fixed point theorem. One version of this states that if you have a continuous function f from a closed n-ball (eg the set of points of distance =< 1 from the origin in n-dimensional Euclidean space) to itself, then this function must have a fixed point, which is an x such that f(x)=x.
So in one dimension, this says that a continuous function f defined on the interval [0,1] that takes values in [0,1] must have a fixed point. (The 1-d version can be proved at high school level, try it!)
Fixed point theorems can have some pretty whack consequence. Eg, if I am in Russia and I put a map of Russia on a table, there will be a point on this map that lies directly above the actual physical spot in Russia that it represents.
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Interesting mathematical statements (1 Viewer)
- Thread starter Paradoxica
- Start date
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Haha yes, spot on with it being a crucial ingredient in Nash's work. This is one of the applications in abstract maths I referred to in my last line which I added after you took your quote.Was the Brouwer fixed point theorem used by Nash to prove the existence of a Nash Equilibrium in a game or something? I don't know too much about game theory haha but this was something I think I heard. And is your Russia thing at all a subtle reference to this game theory of Nash's time) Lol (seems too coincidental that you chose Russia)
And nope, not an intentional reference. Russia was actually an arbitrary choice lol.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
100 people are standing on the positive real axis looking in the positive direction, each wearing hats coloured either black or white.
Each person can see infinitely far and hear from infinite distances.
Going in increasing order, these people are asked the colour of the hat on their head. (They are allowed to discuss a strategy before this whole guessing process starts).
It is slightly surprising that there is a strategy that guarantees correct guesses from 99 of these people.
What is slight more surprising is that these is still such a strategy if more hat colours are allowed (even an uncountable infinitude of hat colours!)
What is most surprising of all is that if there are countably infinite people in this line, and each of these people is deaf, AND there is an uncountable infinity of possible hat colours, we can STILL guarantee the correctness of all but finitely many guesses!!
This is another example of a consequence of the axiom of choice that some people often find unsettling. It also relies on the impossible assumption that a person can have infinite memory...ie they can recall infinite sets, functions on infinite sets, etc etc.
Removing the human / real world element though and viewing the result purely abstractly, it is still immensely weird.
Each person can see infinitely far and hear from infinite distances.
Going in increasing order, these people are asked the colour of the hat on their head. (They are allowed to discuss a strategy before this whole guessing process starts).
It is slightly surprising that there is a strategy that guarantees correct guesses from 99 of these people.
What is slight more surprising is that these is still such a strategy if more hat colours are allowed (even an uncountable infinitude of hat colours!)
What is most surprising of all is that if there are countably infinite people in this line, and each of these people is deaf, AND there is an uncountable infinity of possible hat colours, we can STILL guarantee the correctness of all but finitely many guesses!!
This is another example of a consequence of the axiom of choice that some people often find unsettling. It also relies on the impossible assumption that a person can have infinite memory...ie they can recall infinite sets, functions on infinite sets, etc etc.
Removing the human / real world element though and viewing the result purely abstractly, it is still immensely weird.
Paradoxica
-insert title here-
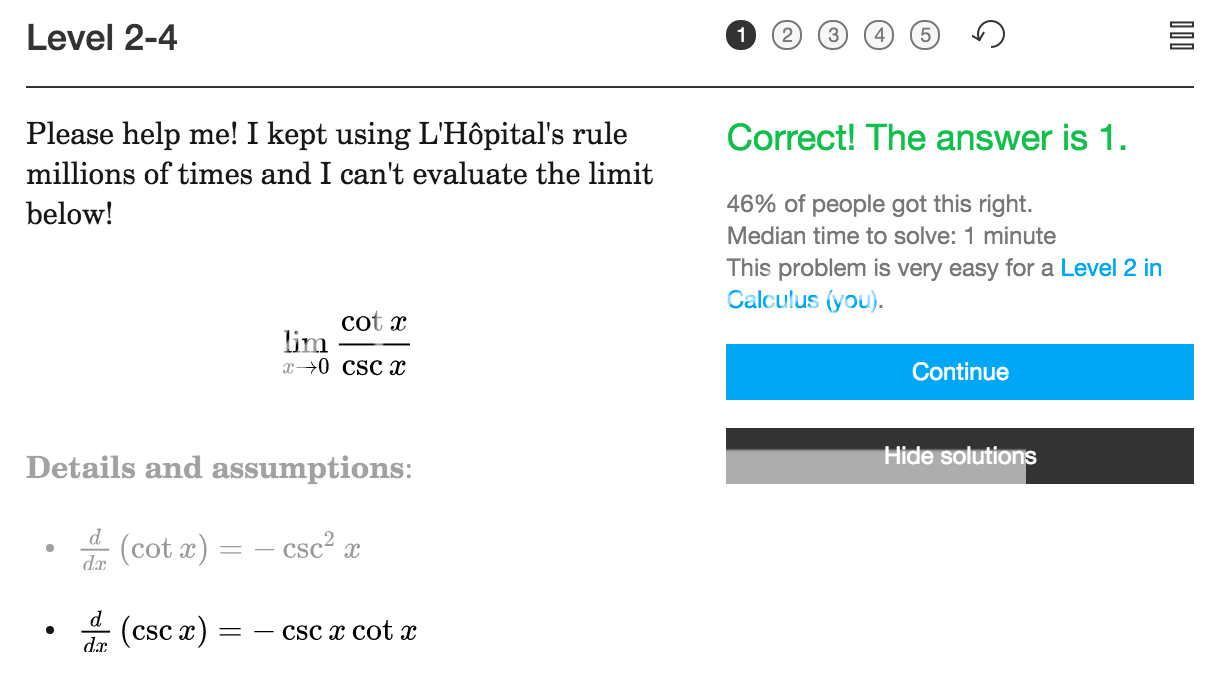
that is rather amusing.
I have seen people do the same for exponential limits.
Paradoxica
-insert title here-
KingOfActing
lukewarm mess
I don't know if anyone's posted this yet:

Any EARLIER Fibonacci number.Carmichael's theorem:

It wouldn't make any sense without that word.
Paradoxica
-insert title here-
Then the computational extension of the theorem is as follows:I don't know if anyone's posted this yet:

If a (turing complete) machine can decide whether or not any given input will halt or not, then said machine cannot decide the input comprising itself.
By the law of the excluded middle, this is a contradiction, and as such, any such machine cannot possibly exist.
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
I don't think this statement is quite true. Specifically, the "input comprising itself" bit - I don't know of a proof that shows that this is the case. If you're alluding to the diagonalisation argument, the result is slightly more complex.Then the computational extension of the theorem is as follows:
If a (turing complete) machine can decide whether or not any given input will halt or not, then said machine cannot decide the input comprising itself.
By the law of the excluded middle, this is a contradiction, and as such, any such machine cannot possibly exist.
Suppose that A is a Turing machine that given any machine T and input I, decides whether B halts on I.
Let C be a machine that, when given I, calls A with machine I and input I and halts iff A concludes that I doesn't halt on input I.
If A is called with machine C and input C and halts, then that means that A must halt on C when given C. Inversely if A is called with (C, C) and doesn't halt, then that means A must halt on (C, C). Here lies the contradiction. (unless I've made a mistake)
So C is the input that breaks T, not T. Unless I've misunderstood what you've said.
But the more important question is - who are you? What kind of high school kid has this kind of background in maths? Where did you learn this stuff?
KingOfActing
lukewarm mess
He's more gay for maths than leehuanI don't think this statement is quite true. Specifically, the "input comprising itself" bit - I don't know of a proof that shows that this is the case. If you're alluding to the diagonalisation argument, the result is slightly more complex.
Suppose that A is a Turing machine that given any machine T and input I, decides whether B halts on I.
Let C be a machine that, when given I, calls A with machine I and input I and halts iff A concludes that I doesn't halt on input I.
If A is called with machine C and input C and halts, then that means that A must halt on C when given C. Inversely if A is called with (C, C) and doesn't halt, then that means A must halt on (C, C). Here lies the contradiction. (unless I've made a mistake)
So C is the input that breaks T, not T. Unless I've misunderstood what you've said.
But the more important question is - who are you? What kind of high school kid has this kind of background in maths? Where did you learn this stuff?
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Oi!He's more gay for maths than leehuan
Paradoxica
-insert title here-
That's why I said comprising. There are a few gaps that I wasn't bothered filling in, because I know the input requires two machines in order to break the supposed machine.I don't think this statement is quite true. Specifically, the "input comprising itself" bit - I don't know of a proof that shows that this is the case. If you're alluding to the diagonalisation argument, the result is slightly more complex.
Suppose that A is a Turing machine that given any machine T and input I, decides whether B halts on I.
Let C be a machine that, when given I, calls A with machine I and input I and halts iff A concludes that I doesn't halt on input I.
If A is called with machine C and input C and halts, then that means that A must halt on C when given C. Inversely if A is called with (C, C) and doesn't halt, then that means A must halt on (C, C). Here lies the contradiction. (unless I've made a mistake)
So C is the input that breaks T, not T. Unless I've misunderstood what you've said.
But the more important question is - who are you? What kind of high school kid has this kind of background in maths? Where did you learn this stuff?
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
You're an IMO guy/girl aren't you?That's why I said comprising. There are a few gaps that I wasn't bothered filling in, because I know the input requires two machines in order to break the supposed machine.
Paradoxica
-insert title here-
If only I were...You're an IMO guy/girl aren't you?
wannaspoon
ремове кебаб
- Joined
- Aug 8, 2012
- Messages
- 1,401
- Gender
- Male
- HSC
- 2007
- Uni Grad
- 2014
actually = 1, but anyway-1 x -1 = 2