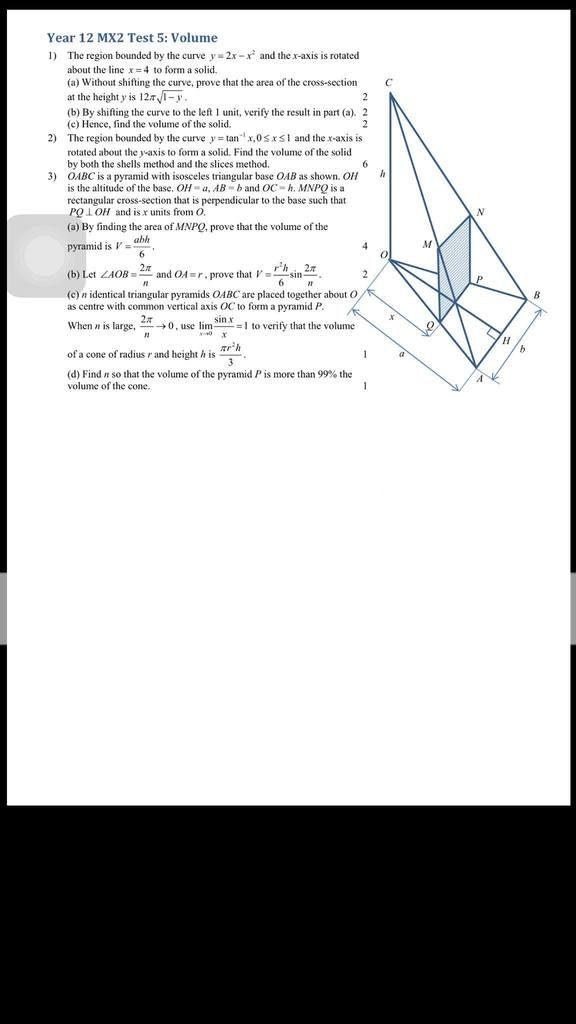
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
leehuan's All-Levels-Of-Maths SOS thread (1 Viewer)
- Thread starter leehuan
- Start date
- Status
- Not open for further replies.
Last edited:
They probably wouldn't mind in MX2 if you just assumed it was monotonically increasing, unless that Q. was worth a lot of marks.Seems a bit rigorous though to test for values... even though yes this is an MX2 question...
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
What scares me is that it was worth 1mk.They probably wouldn't mind in MX2 if you just assumed it was monotonically increasing, unless that Q. was worth a lot of marks.
Paradoxica
-insert title here-
They probably wanted you to exhaustively search for n. That's my best guess. Integrand's method is slightly more exact than what they wanted, but it is correct none the less.What scares me is that it was worth 1mk.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
By symmetry about the y-axis, it suffices to show the circle just passes through S.Another MX2 problem
Progress:
$ but I'm not prepared to. Substituting the centre of the circle does not yield a very nice perfect square to be expanded, requiring a ${4}^{$th$}$ degree. But with GeoGebra's aid I know my results are definitely not wrong. So is there a shortcut I missed at one point that can avoid this brute force? )
Since AB is the diameter of our circle, it suffices to show ASB is a right angle, which you can do just by multiplying gradients of AS and BS.
This does it v.quickly.
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Of course! I was hoping that someone would find a circle geometry trick for me. Thanks!By symmetry about the y-axis, it suffices to show the circle just passes through S.
Since AB is the diameter of our circle, it suffices to show ASB is a right angle, which you can do just by multiplying gradients of AS and BS.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
help pls

Edit: Note that we have skirted over the issue of existence and uniqueness of a solution, as we are not given enough information about S or boundary conditions at infinity for this PDE to be well posed. (Note that adding
Last edited:
I can't quit BoS I need seanieg and InteGrand and co.
Is this correct? If so, is there a neater way to express this?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Paradoxica
-insert title here-
I mean yes that is technically the domain but... it doesn't directly tell you the range of x
Shuuya
Well-Known Member
- Joined
- Sep 3, 2015
- Messages
- 829
- Gender
- Undisclosed
- HSC
- 2016
Welcome back hahaI can't quit BoS I need seanieg and InteGrand and co.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Well, I suppose, what Paradoxica said. But true you have a point
Ah I see. Thanks.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Lol thanks. But I'm only residing in a few sections of the forum for the most part.Welcome back haha
- Status
- Not open for further replies.