-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2017 MX2 Integration Marathon (archive) (1 Viewer)
- Thread starter leehuan
- Start date
- Status
- Not open for further replies.
BenHowe
Active Member
- Joined
- Aug 20, 2015
- Messages
- 354
- Gender
- Male
- HSC
- 2016
- Uni Grad
- 2020
Re: HSC 2017 MX2 Integration Marathon
How do I find what it converges to?
Last edited:
Re: HSC 2017 MX2 Integration Marathon
 \prod_{k=1}^{N} \cos \left(\frac{x}{2^{k}}\right)$ for all positive integers $N$.$)
Here's a hint.How do find what it converges to?
BenHowe
Active Member
- Joined
- Aug 20, 2015
- Messages
- 354
- Gender
- Male
- HSC
- 2016
- Uni Grad
- 2020
Re: HSC 2017 MX2 Integration Marathon
d\theta)
Is there a trick forHere's a much easier one.
Find.
Re: HSC 2017 MX2 Integration Marathon
Yeah, if you call it a trick.Is there a trick ford\theta)
BenHowe
Active Member
- Joined
- Aug 20, 2015
- Messages
- 354
- Gender
- Male
- HSC
- 2016
- Uni Grad
- 2020
Re: HSC 2017 MX2 Integration Marathon
I still dont understand how to do itHere's a hint.
Re: HSC 2017 MX2 Integration Marathon
See this document: https://www.math.ubc.ca/~feldman/m121/secx.pdf .Is there a trick ford\theta)
Re: HSC 2017 MX2 Integration Marathon

I still dont understand how to do it
Re: HSC 2017 MX2 Integration Marathon
}$. Taking the limit as $N\to \infty$ shows that the infinite product is $\frac{\sin x}{x}$, using the fact that $\lim_{N\to \infty} 2^{N}\sin \left( \frac{x}{2^{N}}\right) = x$.$)
I still dont understand how to do it
BenHowe
Active Member
- Joined
- Aug 20, 2015
- Messages
- 354
- Gender
- Male
- HSC
- 2016
- Uni Grad
- 2020
Re: HSC 2017 MX2 Integration Marathon
You are legit so good at this stuff and have awesome resources... Wish you were my maths teacher for HSCSee this document: https://www.math.ubc.ca/~feldman/m121/secx.pdf .
Paradoxica
-insert title here-
Paradoxica
-insert title here-
Re: HSC 2017 MX2 Integration Marathon
^2})
Method one: Exhaustive Partial Fractions. Exercise left to the reader who is bothered.
Method two: Mixed Partial Fractions and a trick substitution.
Observe that\right)$)
Replace this into the numerator and split the integral into two parts.
^2} \, \text{d}s + \int \frac{1}{1-s^2})
Note that for the part that still has the perfect square on the denominator, upon dividing the entire fraction by s², the numerator is the derivative of s-s⁻¹, which is simply the reverse chain rule. The part which is now a simple quadratic is a matter of partial fractions, which is easily done by inspection.
}{\left(s-\frac{1}{s}\right)^2} + \frac{1}{2} \int \frac{1}{1+s} + \frac{1}{1-s} \, \text{d}s = -\frac{1}{s-\frac{1}{s}} + \frac{1}{2}\log{\left(\frac{1+s}{1-s}\right)} )
^2} = \sec{\theta}\tan{\theta} + \log{(\sec{\theta}+\tan{\theta})})
Constant of integration omitted for brevity
Here's a trick method, I suppose...Is there a trick ford\theta)
Method one: Exhaustive Partial Fractions. Exercise left to the reader who is bothered.
Method two: Mixed Partial Fractions and a trick substitution.
Observe that
Replace this into the numerator and split the integral into two parts.
Note that for the part that still has the perfect square on the denominator, upon dividing the entire fraction by s², the numerator is the derivative of s-s⁻¹, which is simply the reverse chain rule. The part which is now a simple quadratic is a matter of partial fractions, which is easily done by inspection.
Constant of integration omitted for brevity
Re: HSC 2017 MX2 Integration Marathon

^2} \, dx $ as follows$)

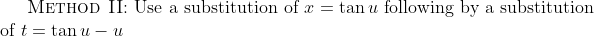
 = x \cos x$, use integration by parts.$)
So when should I remember to see if this works (the reverse quotient rule)?
Last edited:
Re: HSC 2017 MX2 Integration Marathon
Don't see why not. Not something clandestine, is it?Wait, so are we allowed to use methods not known in the HSC Syllabus? That would make everything so much easier
Paradoxica
-insert title here-
Re: HSC 2017 MX2 Integration Marathon
The answer returned by Mathematica is
xlog(1+e^x) + DiLog(-e^x) +C
The DiLogarithm is non-elementary and can only be simplified under specific circumstances, none of which are met by this integral.
That doesn't work, it's still a non-elementary integral.
The answer returned by Mathematica is
xlog(1+e^x) + DiLog(-e^x) +C
The DiLogarithm is non-elementary and can only be simplified under specific circumstances, none of which are met by this integral.
Paradoxica
-insert title here-
Re: HSC 2017 MX2 Integration Marathon
For example, one of the questions I was given technically required the monotone convergence theorem/dominated convergence theorem, in order for the question's proof to be valid, which I cited, and was marked as correct.
Just make sure they can't find any microscopic flaws in your argument, as nobody knows how strict the HSC markers are with extracurricular mathematical reasoning.
As long as it's not dependent on circular assumptions or unproven results (so preferably, has multiple proofs, hopefully some elementary ones), my head teacher told me that I was free to use any theorems I wanted to, that didn't assume the truth of some or all of the question you were going to use it on.Wait, so are we allowed to use methods not known in the HSC Syllabus? That would make everything so much easier
For example, one of the questions I was given technically required the monotone convergence theorem/dominated convergence theorem, in order for the question's proof to be valid, which I cited, and was marked as correct.
Just make sure they can't find any microscopic flaws in your argument, as nobody knows how strict the HSC markers are with extracurricular mathematical reasoning.
Re: HSC 2017 MX2 Integration Marathon
That's why I'm planning to use only known methods in my HSC externals. I asked the head teacher and I'm allowed to use any method as long as they have formal documentation on it and it leads to the answer (For ex. Heaviside Cover Up)As long as it's not dependent on circular assumptions or unproven results (so preferably, has multiple proofs, hopefully some elementary ones), my head teacher told me that I was free to use any theorems I wanted to, that didn't assume the truth of some or all of the question you were going to use it on.
For example, one of the questions I was given technically required the monotone convergence theorem/dominated convergence theorem, in order for the question's proof to be valid, which I cited, and was marked as correct.
Just make sure they can't find any microscopic flaws in your argument, as nobody knows how strict the HSC markers are with extracurricular mathematical reasoning.
Re: HSC 2017 MX2 Integration Marathon
Which methods are you talking about? Inspection in general should be fine (might depend on wording of question), and you could differentiate your answer for indefinite integrals if you wanted to show 'working'.Wait, so are we allowed to use methods not known in the HSC Syllabus? That would make everything so much easier
- Status
- Not open for further replies.

