altSwift
Member
- Joined
- Jan 6, 2017
- Messages
- 65
- Gender
- Male
- HSC
- 2018
Re: HSC 2018 MX2 Marathon
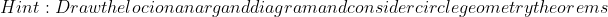
ya rip me. i misinterpreted what z as a variable point meant. i thought it meant z could be anything and that the line was dependent on what z was; although that doesnt make much sense once you think about it.



